题目内容
已知⊙O的半径为
,AB是⊙O的直径,半径CO⊥AB,P为CO的中点,弦BD过点P,则BD= .
| 3 |
考点:圆周角定理,相似三角形的判定与性质
专题:
分析:首先根据题意画出图形,然后由⊙O的半径为
,AB是⊙O的直径,半径CO⊥AB,P为CO的中点,求得PB的长,易证得△POB∽△ADB,然后由相似三角形的对应边成比例求得答案.
| 3 |
解答: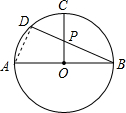 解:连接AD,
解:连接AD,
∵半径CO⊥AB,
∴∠POB=90°,
∵OB=
,OP=
OC=
,
∴PB=
=
,
∵AB是⊙O的直径,
∴∠D=90°,
∴∠D=∠POB,
∵∠B=∠B,
∴△POB∽△ADB,
∴BD:BO=AB:PB,
∴BD=
.
故答案为:
.
 解:连接AD,
解:连接AD,∵半径CO⊥AB,
∴∠POB=90°,
∵OB=
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴PB=
| OB2+OP2 |
| ||
| 2 |
∵AB是⊙O的直径,
∴∠D=90°,
∴∠D=∠POB,
∵∠B=∠B,
∴△POB∽△ADB,
∴BD:BO=AB:PB,
∴BD=
4
| ||
| 5 |
故答案为:
4
| ||
| 5 |
点评:此题考查了圆周角定理以及相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若x1,x2是一元二次方程x2-x-1=0的两根,则x1x2的值是( )
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
下列运算正确的是( )
| A、a+b-(a-b)=0 | ||||||
B、5
| ||||||
| C、(m-1)(m+2)=m2-m+2 | ||||||
| D、(-1)2010-1=2009 |
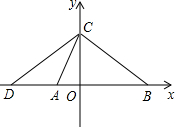 如图,在平面直角坐标系中,直线y=2x+4与x轴交于点A,与y轴交于点C,过点C与AC垂直的直线交x轴于点B,在x轴负半轴上取一点D,使AD=OC,连接CD.
如图,在平面直角坐标系中,直线y=2x+4与x轴交于点A,与y轴交于点C,过点C与AC垂直的直线交x轴于点B,在x轴负半轴上取一点D,使AD=OC,连接CD.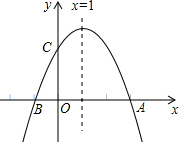 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(-1,0).则下面的四个结论:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(-1,0).则下面的四个结论: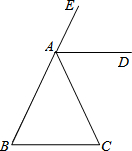 如图,AD是△ABC的外角∠EAC的平分线,且AD∥BC.
如图,AD是△ABC的外角∠EAC的平分线,且AD∥BC.