题目内容
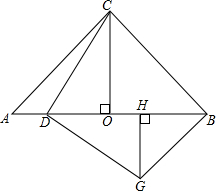在等腰Rt△ABC中，∠ACB=90°，CO⊥AB，D为AO上一点，过点D作CD的垂线，过B点作BC的垂线，两垂线交于的G，过G作GH⊥AB，求证：CO=DH．考点：全等三角形的判定与性质,等腰直角三角形,解直角三角形
专题：证明题
分析：根据等腰直角三角形的性质，可得CO=AO=BO，根据等角的正切值相等，可得
=
，可得OD=BH=GH，根据全等三角形的判定与性质，可得答案．
| b |
| a |
| a+b-x |
| x |
解答：证明：∵等腰Rt△ABC中，∠ACB=90°，CO⊥AB，
∴CO=AO=BO．
∵GD⊥CD，GB⊥BC，GH⊥AB，CO⊥AB，
∴∠OBC=∠GBH═45°=∠BGH．
∵GH=BH，
∴∠CDG=∠CBG=∠GHD=90°，
∴∠DCO∠=GDH，
∴tan∠DCO=tan∠GDH．
设CO=AO=BO=a；OD=b，BH=GH=x，
∴tan∠DCO=
=
，
tan∠DCH=
=
=
，
∴
=
，
bx=a（a+b）-ax，
∴（a+b）x=a（a+b）
x=a，
即：OD=BH=GH
在Rt△DOC和Rt△GHD中，
，
∴△DOC≌△GHD（AAS），
∴CO=DH．
∴CO=AO=BO．
∵GD⊥CD，GB⊥BC，GH⊥AB，CO⊥AB，
∴∠OBC=∠GBH═45°=∠BGH．
∵GH=BH，
∴∠CDG=∠CBG=∠GHD=90°，
∴∠DCO∠=GDH，
∴tan∠DCO=tan∠GDH．
设CO=AO=BO=a；OD=b，BH=GH=x，
∴tan∠DCO=
| CD |
| CO |
| b |
| a |
tan∠DCH=
| GH |
| DH |
| OD+OB-BH |
| GH |
| a+b-x |
| x |
∴
| b |
| a |
| a+b-x |
| x |
bx=a（a+b）-ax，
∴（a+b）x=a（a+b）
x=a，
即：OD=BH=GH
在Rt△DOC和Rt△GHD中，
|
∴△DOC≌△GHD（AAS），
∴CO=DH．
点评：本题考查了全等三角形的判定与性质，利用了等腰直角三角形的性质，等角的正切值相等，全等三角形的判定与性质．
练习册系列答案
阅读快车系列答案
相关题目
下列运算正确的是（ ）
| A、a+b-（a-b）=0 | ||||||
B、5
| ||||||
| C、（m-1）（m+2）=m2-m+2 | ||||||
| D、（-1）2010-1=2009 |