题目内容
19.因式分解:(1)a2b2-a2-2ab-b2
(2)x3-x2y+xy2-y3
(3)(ax-by)2+(bx+ay)2
(4)(x2-4y2)+(4y-1)
分析 (1)将后三项分组进而利用完全平方公式以及平方差公式分解因式得出即可;
(2)将前两项以及后两项分别分组进而提取公因式分解因式即可;
(3)首先利用完全平方公式去括号,再利用分组分解法分解因式即可;
(4)首先去括号,进而将后三项组合,利用完全平方公式以及平方差公式分解因式即可.
解答 解:(1)a2b2-a2-2ab-b2
=a2b2-(a+b)2
=(ab+a+b)(ab-a-b);
(2)x3-x2y+xy2-y3
=x2(x-y)+y2(x-y)
=(x-y)(x2+y2);
(3)(ax-by)2+(bx+ay)2
=a2x2+b2y2-2abxy+b2x2+a2y2+2abxy
=x2(a2+b2)+y2(a2+b2)
=(a2+b2)(x2+y2);
(4)(x2-4y2)+(4y-1)
=x2-(2y-1)2
=(x-2y+1)(x+2y-1).
点评 此题主要考查了公式法以及分组分解法分解因式,正确分组得出是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
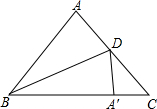 如图,△ABC中,AB=AC=5cm,BC=6cm,BD平分∠ABC,BD交AC于点D,如果将△ABD沿BD翻折,点A落在点A′处,那么△DA′C的面积为$\frac{12}{11}$cm2.
如图,△ABC中,AB=AC=5cm,BC=6cm,BD平分∠ABC,BD交AC于点D,如果将△ABD沿BD翻折,点A落在点A′处,那么△DA′C的面积为$\frac{12}{11}$cm2.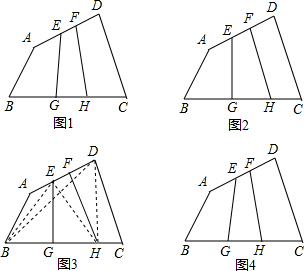 【提出问题】如图①,在四边形ABCD中,点E、F是AD的n等分点中最中间2个,点G、H是BC的n等分点中最中间2个,(其中n为奇数),连接EG、FH,那么S四边形EFHG与S四边形ABCD之间有什么关系呢?
【提出问题】如图①,在四边形ABCD中,点E、F是AD的n等分点中最中间2个,点G、H是BC的n等分点中最中间2个,(其中n为奇数),连接EG、FH,那么S四边形EFHG与S四边形ABCD之间有什么关系呢?