题目内容
12.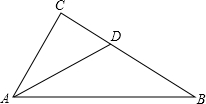 如图,在三角形ABC中,∠C=90度,AD是角平分线,CD=1.5,BD=2.5,求AC的长.
如图,在三角形ABC中,∠C=90度,AD是角平分线,CD=1.5,BD=2.5,求AC的长.
分析 过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得CD=DE,再利用勾股定理列式求出BE,然后求出△ABC和△DBE相似,根据相似三角形对应边成比例列式计算即可得解.
解答  解:过点D作DE⊥AB于E,
解:过点D作DE⊥AB于E,
∵∠C=90度,AD是角平分线,
∴CD=DE,
由勾股定理得,BE=$\sqrt{B{D}^{2}-D{E}^{2}}$=$\sqrt{2.{5}^{2}-1.{5}^{2}}$=2,
∵∠ABC=∠DBE,∠C=∠BED=90°,
∴△ABC∽△DBE,
∴$\frac{AC}{DE}$=$\frac{BC}{BE}$,
即$\frac{AC}{1.5}$=$\frac{1.5+2.5}{2}$,
解得AC=3.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,相似三角形的判定与性质,熟记性质并考虑利用相似三角形求解是解题的关键.

练习册系列答案
相关题目
7.如图所示,是一列用若干火柴棒摆成的由正三角形组成的图案:
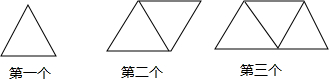
(1)完成下表的填空
(2)某同学用若干火柴棒按如上图所列的方式摆图案,摆完了第1个后,摆第2个,按着摆第3个,…,摆完第n个后剩下22根火柴棒,当他摆完第n+1个图案还多1根,问最后摆的图案是第几个图案?

(1)完成下表的填空
| 正三角形个数 | 1 | 2 | 3 | 4 | … | n |
| 火柴棒根数 | 3 | 5 | 7 | 9 | … | 2n+1 |

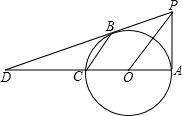 以AC=6为直径画一个圆,过点A作AP⊥AC,过点C作CB∥OP,直线PB与直线AC相交于点D.
以AC=6为直径画一个圆,过点A作AP⊥AC,过点C作CB∥OP,直线PB与直线AC相交于点D.