题目内容
12.已知(19x-31)(13x-17)-( 17-13x)(11x-23)可因式分解成(ax+b)(30x+c),其中a、b、c均为整数,求a+b+c的值.分析 首先将原式提取公因式,进而得出a,b,c的值求出即可.
解答 解:(19x-31)(13x-17)-( 17-13x)(11x-23)
=(19x-31)(13x-17)+( 13x-17)(11x-23)
=(13x-17)(30x-54)
∴a=13,b=-17,c=-54,
∴a+b+c=-58.
点评 此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.

练习册系列答案
相关题目
20. 四个规模不同的滑梯A,B,C,D,它们的滑板长(平直的)分别为300m,250m,200m,200m;滑板与地面所成的角度分别为30°,45°,45°,60°,则关于四个滑梯的高度正确说法( )
四个规模不同的滑梯A,B,C,D,它们的滑板长(平直的)分别为300m,250m,200m,200m;滑板与地面所成的角度分别为30°,45°,45°,60°,则关于四个滑梯的高度正确说法( )
 四个规模不同的滑梯A,B,C,D,它们的滑板长(平直的)分别为300m,250m,200m,200m;滑板与地面所成的角度分别为30°,45°,45°,60°,则关于四个滑梯的高度正确说法( )
四个规模不同的滑梯A,B,C,D,它们的滑板长(平直的)分别为300m,250m,200m,200m;滑板与地面所成的角度分别为30°,45°,45°,60°,则关于四个滑梯的高度正确说法( )| A. | A的最高 | B. | B的最高 | C. | C的最高 | D. | D的最高 |
7.在Rt△ABC中,∠C=90°,AC:BC=1:2,则sinB的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
17.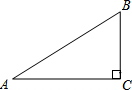 如图,已知在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则AB的长是( )
如图,已知在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则AB的长是( )
 如图,已知在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则AB的长是( )
如图,已知在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则AB的长是( )| A. | 2 | B. | 8 | C. | 2$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
4.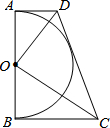 如图,在直角梯形ABCD中AD∥BC.∠ABC=90°DC与以AB为直径的半圆⊙O相切,⊙O的半径为r,在下列结论:①OD⊥OC;②AD+BC=DC; ③S△AOD+S△BOC=S△DOC; ④AD•BC=r2中正确的个数有( )
如图,在直角梯形ABCD中AD∥BC.∠ABC=90°DC与以AB为直径的半圆⊙O相切,⊙O的半径为r,在下列结论:①OD⊥OC;②AD+BC=DC; ③S△AOD+S△BOC=S△DOC; ④AD•BC=r2中正确的个数有( )
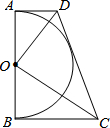 如图,在直角梯形ABCD中AD∥BC.∠ABC=90°DC与以AB为直径的半圆⊙O相切,⊙O的半径为r,在下列结论:①OD⊥OC;②AD+BC=DC; ③S△AOD+S△BOC=S△DOC; ④AD•BC=r2中正确的个数有( )
如图,在直角梯形ABCD中AD∥BC.∠ABC=90°DC与以AB为直径的半圆⊙O相切,⊙O的半径为r,在下列结论:①OD⊥OC;②AD+BC=DC; ③S△AOD+S△BOC=S△DOC; ④AD•BC=r2中正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
1. 如图,PA、PB是⊙O的切线,AC是⊙O的直径,∠P=62°,则∠BOC的度数为( )
如图,PA、PB是⊙O的切线,AC是⊙O的直径,∠P=62°,则∠BOC的度数为( )
 如图,PA、PB是⊙O的切线,AC是⊙O的直径,∠P=62°,则∠BOC的度数为( )
如图,PA、PB是⊙O的切线,AC是⊙O的直径,∠P=62°,则∠BOC的度数为( )| A. | 60° | B. | 62° | C. | 31° | D. | 70° |
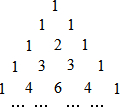 如图所示的“贾宪三角”告诉了我们二项式乘方展开式的系数规律,如:第四行的四个数恰好对应着(a+b)3的展开式a3+3a2b+3ab2+b3的系数; 第五行的五个数恰好对应着(a+b)4的展开式a4+4a3b+6a2b2+4ab3+b4的系数;
如图所示的“贾宪三角”告诉了我们二项式乘方展开式的系数规律,如:第四行的四个数恰好对应着(a+b)3的展开式a3+3a2b+3ab2+b3的系数; 第五行的五个数恰好对应着(a+b)4的展开式a4+4a3b+6a2b2+4ab3+b4的系数;