题目内容
2.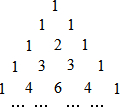 如图所示的“贾宪三角”告诉了我们二项式乘方展开式的系数规律,如:第四行的四个数恰好对应着(a+b)3的展开式a3+3a2b+3ab2+b3的系数; 第五行的五个数恰好对应着(a+b)4的展开式a4+4a3b+6a2b2+4ab3+b4的系数;
如图所示的“贾宪三角”告诉了我们二项式乘方展开式的系数规律,如:第四行的四个数恰好对应着(a+b)3的展开式a3+3a2b+3ab2+b3的系数; 第五行的五个数恰好对应着(a+b)4的展开式a4+4a3b+6a2b2+4ab3+b4的系数;根据数表中前五行的数字所反映的规律,回答:
(1)图中第七行正中间的数字是20;
(2)(a+b)6的展开式是a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6.
分析 (1)观察图表寻找规律:三角形是一个由数字排列成的三角形数表,它的两条斜边都是数字1组成,而其余的数则是等于它“肩”上的两个数之和,进而得出答案;
(2)利用(1)中所求即可得出答案.
解答 解:(1)可以发现:(a+b)n的各项展开式的系数除首尾两项都是1外,其余各项系数都等于(a+b)n-1的相邻两个系数的和,
则(a+b)4的各项系数依次为1、4、6、4、1;
(a+b)5的各项系数依次为1、5、10、10、5、1;
则(a+b)6的系数分别为1、6、15、20、15、6、1.
故第七行正中间的数字是:20;
故答案为:20;
(2)由(1)得:(a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6.
故答案为:a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6.
点评 本题考查了整式的混合运算,学生解决实际问题的能力和阅读理解能力,找出本题的数字规律是正确解题的关键.

练习册系列答案
相关题目
12. 下列选项中能由左图平移得到的是( )
下列选项中能由左图平移得到的是( )
 下列选项中能由左图平移得到的是( )
下列选项中能由左图平移得到的是( )| A. |  | B. |  | C. |  | D. |  |
17.在一个已经装有10个黑色玻璃球的不透明布袋中再装入30个红色、白色玻璃球,这些球除颜色外其他完全相同.小花做摸球实验,她将袋子里面的球充分搅均匀后从中随机摸出一个球记下颜色,再把它放回袋子里,不断重复上述过程,下表是实验中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P白=0.6;
(3)从中选出12个玻璃球设计摸球游戏,使摸到红球的概率和摸到白球的概率相等.
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 67 | 122 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.67 | 0.61 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)假如你摸一次,你摸到白球的概率P白=0.6;
(3)从中选出12个玻璃球设计摸球游戏,使摸到红球的概率和摸到白球的概率相等.
11.直线y=(1-2m)x+m-1,不论m取什么值,该直线必定经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,D是线段AC的中点,E是线段AB的中点.已知AB=10,BC=3,求线段AD和DE的长度.
如图,D是线段AC的中点,E是线段AB的中点.已知AB=10,BC=3,求线段AD和DE的长度.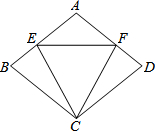 如图,等腰△CEF的两腰CE、CF的长与菱形ABCD的边长相等.
如图,等腰△CEF的两腰CE、CF的长与菱形ABCD的边长相等.