题目内容
4.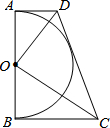 如图,在直角梯形ABCD中AD∥BC.∠ABC=90°DC与以AB为直径的半圆⊙O相切,⊙O的半径为r,在下列结论:①OD⊥OC;②AD+BC=DC; ③S△AOD+S△BOC=S△DOC; ④AD•BC=r2中正确的个数有( )
如图,在直角梯形ABCD中AD∥BC.∠ABC=90°DC与以AB为直径的半圆⊙O相切,⊙O的半径为r,在下列结论:①OD⊥OC;②AD+BC=DC; ③S△AOD+S△BOC=S△DOC; ④AD•BC=r2中正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 设DC和半圆⊙O相切的切点为E,连接OE,根据切线长定理以及相似三角形的判定和性质逐项分析即可.
解答 解:设DC和半圆⊙O相切的切点为E,连接OE,
∵在直角梯形ABCD中AD∥BC.∠ABC=90°,
∴∠DAB=90°,
∵AB为直径,
∴AD,BC是圆的切线,
∵DC与以AB为直径的半圆⊙O相切,
∴AD=DE,BC=CE,
∴AD+BC=DE+CE=DC,故②正确;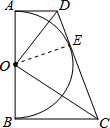
∵∠ADO=∠EDO,
∴∠AOD=∠DOE,
同理:∠BOC=∠EOC,
∴∠DOC=$\frac{1}{2}$(AOE+∠BOE)=90°,
∴OD⊥OC,故①正确;
∵S△AOD=$\frac{1}{2}$AD•AO,S△BOC=$\frac{1}{2}$BO•BC,S△DOC=$\frac{1}{2}$OE•DC,
又∵AO=BO=OE,AD+BC=DC,
∴S△AOD+S△BOC=S△DOC,故③正确;
∵∠A=∠B=90°,∠AOD=∠BCO,
∴△AOD∽△BCO,
∴$\frac{AD}{BO}=\frac{AO}{BC}$,
∴AD•BC=r2,故④正确,
综上可知正确的个数有4个,
故选A.
点评 本题考查了切线的判定和性质、相似三角形的判定与性质、直角三角形的判定与性质.解决本题的关键是熟练掌握相似的三角形判定定理、性质定理,做到灵活运用.

练习册系列答案
相关题目
19.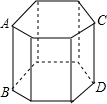 如图,直六棱柱的底面是边长为4cm的正六边形,AB为8cm,则此直六棱柱左视图的面积为( )
如图,直六棱柱的底面是边长为4cm的正六边形,AB为8cm,则此直六棱柱左视图的面积为( )
 如图,直六棱柱的底面是边长为4cm的正六边形,AB为8cm,则此直六棱柱左视图的面积为( )
如图,直六棱柱的底面是边长为4cm的正六边形,AB为8cm,则此直六棱柱左视图的面积为( )| A. | 32$\sqrt{3}$cm2 | B. | 32cm2 | C. | 64cm2 | D. | 16$\sqrt{3}$cm2 |
16.某公园中央地上有一个大理石球,小明想测量球的半径,于是找了两块厚20cm的砖塞在球的两侧(如图所示),他量了下两砖之间的距离刚好是80cm,聪明的你,请你算出大石头的半径是( )


| A. | 40cm | B. | 30cm | C. | 20cm | D. | 50cm |
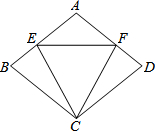 如图,等腰△CEF的两腰CE、CF的长与菱形ABCD的边长相等.
如图,等腰△CEF的两腰CE、CF的长与菱形ABCD的边长相等. 雾霾成为“两会”最大的民生话题. 浙江2015年十件民生实事已公布,雾霾治理居首位,杭州市确定了7600亿元的巨额治理投资,将用市场手段治理雾霾.7600亿元,用科学记数法表示为7.6×1011元.
雾霾成为“两会”最大的民生话题. 浙江2015年十件民生实事已公布,雾霾治理居首位,杭州市确定了7600亿元的巨额治理投资,将用市场手段治理雾霾.7600亿元,用科学记数法表示为7.6×1011元.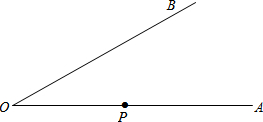 如图所示,已知∠AOB,点P在OA上.
如图所示,已知∠AOB,点P在OA上.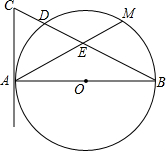 如图,AB是⊙O的直径,AC与⊙O相切于A,连接BC,BC交⊙O于点D,M是弧$\widehat{BD}$的中点,连接AM交BC于点E.
如图,AB是⊙O的直径,AC与⊙O相切于A,连接BC,BC交⊙O于点D,M是弧$\widehat{BD}$的中点,连接AM交BC于点E.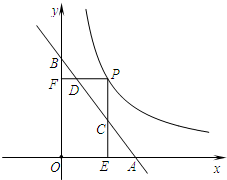 如图所示,直线y=-x+2分别与x轴、y轴交于点A、B,点P为函数y=$\frac{\sqrt{2}}{x}$ (x>0)图象上的一点,过点P分别作x轴、y轴的垂线段PE、PF,当PE、PF分别与线段AB交于点C、D时,则AD•BC的值为2$\sqrt{2}$.
如图所示,直线y=-x+2分别与x轴、y轴交于点A、B,点P为函数y=$\frac{\sqrt{2}}{x}$ (x>0)图象上的一点,过点P分别作x轴、y轴的垂线段PE、PF,当PE、PF分别与线段AB交于点C、D时,则AD•BC的值为2$\sqrt{2}$.