题目内容
3.已知长方形的长为线段a,宽与长之比为黄金比,则这个长方形的面积为$\frac{\sqrt{5}-1}{2}$a2.分析 先由长方形的长为线段a,宽与长之比为黄金比,求出宽为$\frac{\sqrt{5}-1}{2}$a,再利用长方形的面积=长×宽即可求解.
解答 解:∵长方形的长为线段a,宽与长之比为黄金比,
∴宽为$\frac{\sqrt{5}-1}{2}$a,
∴这个长方形的面积=a•$\frac{\sqrt{5}-1}{2}$a=$\frac{\sqrt{5}-1}{2}$a2.
故答案为$\frac{\sqrt{5}-1}{2}$a2.
点评 本题考查了黄金分割:把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值($\frac{\sqrt{5}-1}{2}$)叫做黄金比.熟记黄金比的值是解题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
11.直线y=(1-2m)x+m-1,不论m取什么值,该直线必定经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
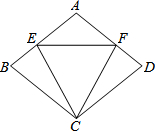 如图,等腰△CEF的两腰CE、CF的长与菱形ABCD的边长相等.
如图,等腰△CEF的两腰CE、CF的长与菱形ABCD的边长相等. 雾霾成为“两会”最大的民生话题. 浙江2015年十件民生实事已公布,雾霾治理居首位,杭州市确定了7600亿元的巨额治理投资,将用市场手段治理雾霾.7600亿元,用科学记数法表示为7.6×1011元.
雾霾成为“两会”最大的民生话题. 浙江2015年十件民生实事已公布,雾霾治理居首位,杭州市确定了7600亿元的巨额治理投资,将用市场手段治理雾霾.7600亿元,用科学记数法表示为7.6×1011元.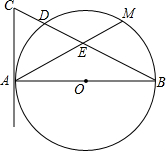 如图,AB是⊙O的直径,AC与⊙O相切于A,连接BC,BC交⊙O于点D,M是弧$\widehat{BD}$的中点,连接AM交BC于点E.
如图,AB是⊙O的直径,AC与⊙O相切于A,连接BC,BC交⊙O于点D,M是弧$\widehat{BD}$的中点,连接AM交BC于点E.