题目内容
4.已知关于x的一元二次方程ax2-(2a+3)x+a+1=0有实数根,则实数a的取值范围是( )| A. | a>-$\frac{9}{8}$ | B. | a≥-$\frac{9}{8}$ | C. | a≥-$\frac{9}{8}$且a≠0 | D. | a>-$\frac{9}{8}$且a≠0 |
分析 方程要有实数根,则根的判别式△≥0,且二次项系数不为零,建立关于a的不等式,求解即可.
解答 解:由题意知:a≠0,
∵△=b2-4ac=[-(2a-3)]2-4×a×(a+1)≥0,
∴解得a≥-$\frac{9}{8}$.
故选:C.
点评 此题考查一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.注意一元二次方程中,二次项系数不能为0.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
12.下列运算正确的是( )
| A. | a-2a=a | B. | (-a2)3=-a6 | C. | a6÷a3=a2 | D. | a3-a2=a |
16.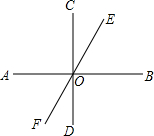 如图所示,直线AB,CD,EF相交于点O,且AB⊥CD于点O,∠BOE=70°,则∠FOD等于( )
如图所示,直线AB,CD,EF相交于点O,且AB⊥CD于点O,∠BOE=70°,则∠FOD等于( )
 如图所示,直线AB,CD,EF相交于点O,且AB⊥CD于点O,∠BOE=70°,则∠FOD等于( )
如图所示,直线AB,CD,EF相交于点O,且AB⊥CD于点O,∠BOE=70°,则∠FOD等于( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |