题目内容
14.两个相似多边形,它们的相似比为2:3,若它们的周长之和为15cm,则这两个多边形的面积比为4:9.这两个多边形的周长分别为6cm、9 cm.分析 根据相似多边形面积的比等于相似比的平方易得这两个多边形的面积比为4:9;根据相似多边周长的比等于相似比得到这两个多边形的周长比为2:3,然后利用它们的周长之和为15cm可分别计算出两个多边的周长.
解答 解:∵两个相似多边形的相似比为2:3,
∴这两个多边形的面积比为4:9;
这两个多边形的周长比为2:3,
∴一个多边形的周长=$\frac{2}{5}$×15cm=6cm,另一个多边形的周长=$\frac{3}{5}$×15cm=9cm.
故答案为4:9;6cm、9.
点评 本题考查了相似多边形的性质:相似多边形对应边的比叫做相似比;相似多边形的对应角相等,对应边的比相等;相似多边形面积的比等于相似比的平方.

练习册系列答案
相关题目
9.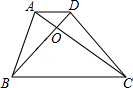 如图,梯形ABCD的对角线AC、BD相交于O,若AD=3,BC=9,则AO:OC=( )
如图,梯形ABCD的对角线AC、BD相交于O,若AD=3,BC=9,则AO:OC=( )
 如图,梯形ABCD的对角线AC、BD相交于O,若AD=3,BC=9,则AO:OC=( )
如图,梯形ABCD的对角线AC、BD相交于O,若AD=3,BC=9,则AO:OC=( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 11:20 |
6.要反映某种股票的涨跌情况,最好选择( )
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 列表 |
3.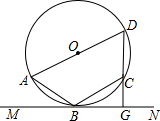 如图所示,已知四边形ABCD为圆内接四边形,AD为圆的直径,直线MN切圆于点B,DC的延长线交MN于G,且cos∠ABM=$\frac{{\sqrt{3}}}{2}$,则tan∠BCG的值为( )
如图所示,已知四边形ABCD为圆内接四边形,AD为圆的直径,直线MN切圆于点B,DC的延长线交MN于G,且cos∠ABM=$\frac{{\sqrt{3}}}{2}$,则tan∠BCG的值为( )
 如图所示,已知四边形ABCD为圆内接四边形,AD为圆的直径,直线MN切圆于点B,DC的延长线交MN于G,且cos∠ABM=$\frac{{\sqrt{3}}}{2}$,则tan∠BCG的值为( )
如图所示,已知四边形ABCD为圆内接四边形,AD为圆的直径,直线MN切圆于点B,DC的延长线交MN于G,且cos∠ABM=$\frac{{\sqrt{3}}}{2}$,则tan∠BCG的值为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
4.已知关于x的一元二次方程ax2-(2a+3)x+a+1=0有实数根,则实数a的取值范围是( )
| A. | a>-$\frac{9}{8}$ | B. | a≥-$\frac{9}{8}$ | C. | a≥-$\frac{9}{8}$且a≠0 | D. | a>-$\frac{9}{8}$且a≠0 |
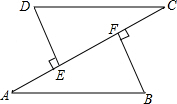 已知:如图,AE=CF,DE⊥AC,BF⊥AC,垂足分别为E,F,DE=BF.求证:AB∥CD.
已知:如图,AE=CF,DE⊥AC,BF⊥AC,垂足分别为E,F,DE=BF.求证:AB∥CD.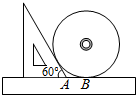 如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的半径是3$\sqrt{3}$cm.
如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的半径是3$\sqrt{3}$cm.