题目内容
9.已知一次函数y=kx-1中,比例系数k满足k=$\frac{c}{a+b}=\frac{a}{b+c}=\frac{b}{c+a}$,试求直线y=kx-1与x轴的交点坐标.分析 首先由k=$\frac{c}{a+b}=\frac{a}{b+c}=\frac{b}{c+a}$,求得k=2,得出函数解析式,进一步令y=0,求得x的数值,得出答案即可.
解答 解:∵k=$\frac{c}{a+b}=\frac{a}{b+c}=\frac{b}{c+a}$,
①当a+b+c=0时,k=-1,
②当a+b+c≠0时,k=$\frac{a+b+c}{2a+2b+2c}$=$\frac{1}{2}$
∴一次函数y=-x-1或y=$\frac{1}{2}$x-1
∴直线y=2x-1与x轴的交点坐标为(2,0)或(-1,0).
点评 此题考查一次函数与坐标轴的交点坐标,比例的基本性质,求得k的数值是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.下列从左到右的变形中,是因式分解的是( )
| A. | x2-6x+9=x(x-6-9) | B. | (a+2)(a-2)=a2-4 | C. | 2a(b-c)=2ab-2bc | D. | y2-4y+4=(y-2)2 |
17.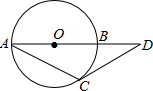 如图,已知⊙O的半径为R,AB是⊙O的直径,D是AB延长线上一点,DC是⊙O的切线,C是切点,连结AC.若∠CAB=30°,则BD的长为( )
如图,已知⊙O的半径为R,AB是⊙O的直径,D是AB延长线上一点,DC是⊙O的切线,C是切点,连结AC.若∠CAB=30°,则BD的长为( )
 如图,已知⊙O的半径为R,AB是⊙O的直径,D是AB延长线上一点,DC是⊙O的切线,C是切点,连结AC.若∠CAB=30°,则BD的长为( )
如图,已知⊙O的半径为R,AB是⊙O的直径,D是AB延长线上一点,DC是⊙O的切线,C是切点,连结AC.若∠CAB=30°,则BD的长为( )| A. | R | B. | $\sqrt{3}$R | C. | 2R | D. | $\frac{\sqrt{3}}{2}$R |
4.已知关于x的一元二次方程ax2-(2a+3)x+a+1=0有实数根,则实数a的取值范围是( )
| A. | a>-$\frac{9}{8}$ | B. | a≥-$\frac{9}{8}$ | C. | a≥-$\frac{9}{8}$且a≠0 | D. | a>-$\frac{9}{8}$且a≠0 |
1.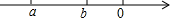 已知,a,b两个实数在数轴上的对应点如图所示,则下列各式一定成立的是( )
已知,a,b两个实数在数轴上的对应点如图所示,则下列各式一定成立的是( )
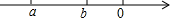 已知,a,b两个实数在数轴上的对应点如图所示,则下列各式一定成立的是( )
已知,a,b两个实数在数轴上的对应点如图所示,则下列各式一定成立的是( )| A. | a-1>b-1 | B. | 3a>3b | C. | -a>-b | D. | a+b>a-b |
 如图所示,二次函数y=x2-x-6的图象交x轴于A、B两点,交y轴于C点,则△ABC的面积S△ABC=15.
如图所示,二次函数y=x2-x-6的图象交x轴于A、B两点,交y轴于C点,则△ABC的面积S△ABC=15.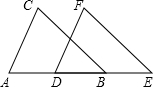 把下面的推理过程补充完整,并在括号内注明理由.如图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF,试说明:(1)∠C=∠F;(2)AC∥DF.
把下面的推理过程补充完整,并在括号内注明理由.如图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF,试说明:(1)∠C=∠F;(2)AC∥DF.