Question

6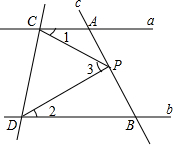．已知：如图，直线a∥b，直线c和直线a、b分别相交于A、B两点，点P在AB上．
（1）猜测∠1、∠2、∠3之间的数量关系并说明理由；
（2）如果点P在A、B两点之间运动时，（1）中∠1、∠2、∠3之间的数量关系是否发生变化（直接写出结果，不需说明理由）；
（3）如果点P在直线c上A、B两点外侧运动（点P与A、B不重合）时，直接写出∠1、∠2、∠3之间的数量关系．

Answer 1

分析 （1）过点P作PE∥a交CD于点E，由PE∥a、a∥b可得PE∥a∥b，根据平行线的性质可得∠1=∠CPE、∠2=∠DPE，结合∠3=∠CPE+∠DPE即可得出∠3=∠1+∠2；
（2）同（1）方法，可得出∠1、∠2、∠3之间的数量关系不会发生变化，即∠3=∠1+∠2；
（3）分点P在A、B两点外侧BA方向运动和点P在A、B两点外侧AB方向运动两种情况考虑，过点P作PF∥a交CD于点F，根据平行线的性质可得∠1=∠CPF、∠2=∠DPF，结合∠3=∠DPF-∠CPF（或∠3=∠CPF-∠DPF）即可得出∠1、∠2、∠3之间的数量关系．

解答 解：（1）∠3=∠1+∠2，理由如下：
过点P作PE∥a交CD于点E，如图1所示．
∵PE∥a，a∥b，
∴PE∥a∥b，
∴∠1=∠CPE，∠2=∠DPE．
∵∠3=∠CPE+∠DPE，
∴∠3=∠1+∠2．
（2）∠1、∠2、∠3之间的数量关系不会发生变化，即∠3=∠1+∠2（理由同（1））．
（3）当点P在A、B两点外侧BA方向运动时，过点P作PF∥a交CD于点F，如图2所示．
∵PF∥a，a∥b，
∴PF∥a∥b，
∴∠1=∠CPF，∠2=∠DPF．
∵∠3=∠DPF-∠CPF，
∴∠3=∠2-∠1．
同理可得：当点P在A、B两点外侧AB方向运动时，∠3=∠1-∠2．

点评 本题考查了平行线的性质，解题的关键是：（1）根据“两直线平行，内错角相等”找出∠1=∠CPE、∠2=∠DPE；（2）根据“两直线平行，内错角相等”找出∠1=∠CPE、∠2=∠DPE；（3）根据“两直线平行，内错角相等”找出∠1=∠CPF、∠2=∠DPF．