题目内容
1.若$\sqrt{x-y}$+y2-4y+4=0,求$\frac{1}{x}$+$\frac{1}{y}$的值.分析 根据非负数的性质可以求得x、y的值,从而可以求得$\frac{1}{x}$+$\frac{1}{y}$的值.
解答 解:$\sqrt{x-y}$+y2-4y+4=0,
∴$\sqrt{x-y}$+(y-2)2=0,
∴$\left\{\begin{array}{l}{x-y=0}\\{y-2=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,
∴$\frac{1}{x}$+$\frac{1}{y}$=$\frac{1}{2}+\frac{1}{2}=1$.
点评 本题考查分式的化简求值、非负数的性质,解答本题的关键是明确分式化简求值的方法,利用非负数的性质解答.

练习册系列答案
相关题目
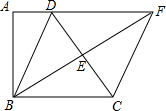 如图,四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
如图,四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长与AD的延长线相交于点F. 把下列各数分别填在相应的集合中:
把下列各数分别填在相应的集合中: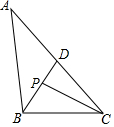 如图,在△ABC中,∠ABC=100°,∠ACB=40°,∠ABC的平分线BD交AC于点D,∠ACB的平分线CP交BD于点D.
如图,在△ABC中,∠ABC=100°,∠ACB=40°,∠ABC的平分线BD交AC于点D,∠ACB的平分线CP交BD于点D.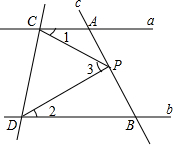 已知:如图,直线a∥b,直线c和直线a、b分别相交于A、B两点,点P在AB上.
已知:如图,直线a∥b,直线c和直线a、b分别相交于A、B两点,点P在AB上.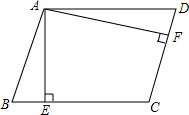 如图,平行四边形ABCD的邻边AD:AB=5:4,过点A作AE⊥BC,AF⊥CD,垂足分别为点E、F,AE=2cm,则AF=2.5cm.
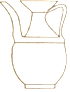
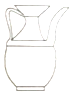
如图,平行四边形ABCD的邻边AD:AB=5:4,过点A作AE⊥BC,AF⊥CD,垂足分别为点E、F,AE=2cm,则AF=2.5cm. 湖南省第二次文物普查时,省考古研究所在冷水滩钱家州征集到一个宋代“青釉瓜棱形瓷执壶”如图所示,该壶为盛酒器,瓷质,侈口,喇叭形长颈,长立把,则该“青釉瓜棱形瓷执壶”的主视图是( )
湖南省第二次文物普查时,省考古研究所在冷水滩钱家州征集到一个宋代“青釉瓜棱形瓷执壶”如图所示,该壶为盛酒器,瓷质,侈口,喇叭形长颈,长立把,则该“青釉瓜棱形瓷执壶”的主视图是( )