题目内容
16．已知$\sqrt{a-1}$+|b2+1|=1，求$\frac{1}{（a+1）（b+1）}$+$\frac{1}{（a+2）（b+2）}$+…+$\frac{1}{（a+2012）（b+2012）}$的值．分析 根据$\sqrt{a-1}$+|b2+1|=1，b2+1≥1可知a=1，b=0，代入原式，把原式写成差的形式计算即可．
解答 解：∵$\sqrt{a-1}$+|b2+1|=1，b2+1≥1，
∴a=1，b=0，
原式=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{2012×2013}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2012}$-$\frac{1}{2013}$
=1-$\frac{1}{2013}$
=$\frac{2012}{2013}$．
点评 本题考查的是求代数式的值，求出a、b的值、找出简单方法计算原式是解题的关键，解答时，要注意非负数的性质的运用．
练习册系列答案
阅读快车系列答案
相关题目
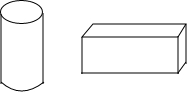如图，某厂生产一种容积为100πL的圆柱形热水器，它的高等于底面直径d的2倍，（1L=1立方分米），厂家为它设计了一种长方体的包装盒，其容积为432L，高为6分米，且长、宽之比为2：1，问这种包装盒能用吗？
已知，在△ABC中，AB=AC，D是BC的中点，BE=CF，求证：△BDE≌△CDF．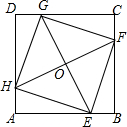
如图，在正方形ABCD中，E、F、G、H分别为边AB、BC、CD、DA上的点，HA=EB=FC=GD，连接EG、FH，交点为O，连接EF、FG、GH、HE，求证：四边形EFGH是正方形．
如图，四边形ABCD中，∠B=∠D=90°，且AB=4，CD=2，∠A=60°，求四边形ABCD的面积．