题目内容
1.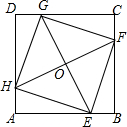 如图,在正方形ABCD中,E、F、G、H分别为边AB、BC、CD、DA上的点,HA=EB=FC=GD,连接EG、FH,交点为O,连接EF、FG、GH、HE,求证:四边形EFGH是正方形.
如图,在正方形ABCD中,E、F、G、H分别为边AB、BC、CD、DA上的点,HA=EB=FC=GD,连接EG、FH,交点为O,连接EF、FG、GH、HE,求证:四边形EFGH是正方形.
分析 先证明△AEH≌△BFE≌△CGF≌△DHG,可得出四边形GHEF是菱形,再根据全等三角形角之间的关系,又可得出菱形的一个角是直角,那么就可得出四边形GHEF是正方形.
解答 证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵HA=EB=FC=GD,
∴AE=BF=CG=DH,
∴△AEH≌△BFE≌△CGF≌△DHG,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形,
∵△DHG≌△AEH,
∴∠DHG=∠AEH,
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∴四边形EFGH是正方形.
点评 本题考查正方形的判定与性质,全等三角形的判定和性质,利用正方形的性质,掌握正方形的判定方法是解决问题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
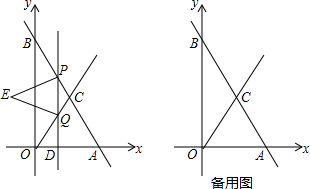
 如图,AB⊥CD于O,直线EF经过点O,OG⊥EF,∠COG=2∠BOE,求∠BOE,∠AOF,∠AOE的度数.
如图,AB⊥CD于O,直线EF经过点O,OG⊥EF,∠COG=2∠BOE,求∠BOE,∠AOF,∠AOE的度数.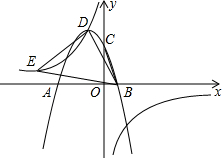 如图,抛物线y=ax2+2ax+c(a≠0)交x轴于点A(-3,0)与点B,与y轴交于点C,tan∠ABC=3,双曲线$y=\frac{k}{x}(k≠0)$经过抛物线的顶点D.
如图,抛物线y=ax2+2ax+c(a≠0)交x轴于点A(-3,0)与点B,与y轴交于点C,tan∠ABC=3,双曲线$y=\frac{k}{x}(k≠0)$经过抛物线的顶点D.