题目内容
8. 如图,四边形ABCD中,∠B=∠D=90°,且AB=4,CD=2,∠A=60°,求四边形ABCD的面积.
如图,四边形ABCD中,∠B=∠D=90°,且AB=4,CD=2,∠A=60°,求四边形ABCD的面积.
分析 延长DC交AB的延长线与点E,根据∠A=60°,∠B=∠D=90°可知∠E=30°,再由锐角三角函数的定义求出CE及BE的长,由勾股定理求出BC的长,进而可得出结论.
解答  解:延长DC交AB的延长线与点E,
解:延长DC交AB的延长线与点E,
∵∠A=60°,∠B=∠D=90°,
∴∠E=30°.
在Rt△BCE中,$\frac{BE}{CE}$=$\frac{\sqrt{3}}{2}$①,
在Rt△ADE中,$\frac{DE}{AE}$=$\frac{2+CE}{4+BE}$=$\frac{\sqrt{3}}{2}$②,
①②联立得,CE=16,BE=8$\sqrt{3}$,
∴BC=$\frac{1}{2}$CE=8,DE=CD+CE=18,
∴AE=AB+BE=4+8$\sqrt{3}$,
∴AD=$\frac{1}{2}$AE=2+4$\sqrt{3}$,
∴S四边形ABCD=S△ADE-S△BCE=$\frac{1}{2}$AD•DE-$\frac{1}{2}$BE•BC=$\frac{1}{2}$×(2+4$\sqrt{3}$)×18-$\frac{1}{2}$×8$\sqrt{3}$×8=18+36$\sqrt{3}$-32$\sqrt{3}$=18+4$\sqrt{3}$.
点评 本题考查的是勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
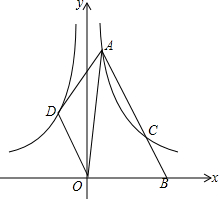 如图,在平面直角坐标系中,点A在第一象限,且其纵坐标为8,点B为x轴正半轴上一点,且tan∠ABO=2,双曲线y=$\frac{k}{x}$(x>0)经过点A,交AB于点C,且AC=3BC.
如图,在平面直角坐标系中,点A在第一象限,且其纵坐标为8,点B为x轴正半轴上一点,且tan∠ABO=2,双曲线y=$\frac{k}{x}$(x>0)经过点A,交AB于点C,且AC=3BC. 如图,已知矩形ABCD,AD=2,CD=5,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.
如图,已知矩形ABCD,AD=2,CD=5,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.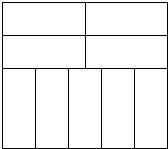 某中学为了提高学生羽毛球水平,准备将一块周长为76m的长方形空地,设计成长、宽分别相等的9块长方形羽毛球场(如图),新建的羽毛球场需要进行装修,已知装修费用为每平方分米1元,问学校要投资多少钱来装修?
某中学为了提高学生羽毛球水平,准备将一块周长为76m的长方形空地,设计成长、宽分别相等的9块长方形羽毛球场(如图),新建的羽毛球场需要进行装修,已知装修费用为每平方分米1元,问学校要投资多少钱来装修?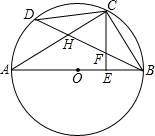 如图,AB是⊙O的直径,C是$\widehat{BD}$的中点,CE⊥AB于E,BD交CE于点F,BD交CA于点H.
如图,AB是⊙O的直径,C是$\widehat{BD}$的中点,CE⊥AB于E,BD交CE于点F,BD交CA于点H.