题目内容
小明在学习轴对称的时候,老师留了这样一道思考题:如图a,若点A,B在直线m同侧,在直线m上找一点P,使得AP+BP的值最小,小明通过独立思考,很快得出了解决这个问题的正确方法,他的做法是这样的:
①作点B关于直线m的对称点B′;②连接AB′,与直线m的交点P,则点P为所求线段AB′的长度即为AP+BP的最小值.
请你参考小明的做法解决下列问题:
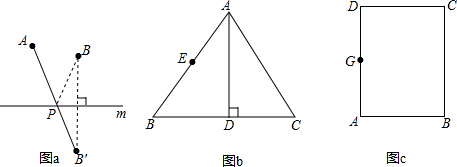
(1)如图b,在等边△ABC中,AB=2,点E是AB的中点,AD是高,在AD上作出点P.(尺规作图,保留作图痕迹,不写作法),使得BP+PE的值最小,并求出最小值;
(2)如图c,在矩形ABCD中,AB=4,BC=6,G为边AD的中点,若E,F为边AB上的两个动点,点E在点F左侧,且EF=1,当四边形CGEF的周长最小时,请你在图c中确定点E,F的位置(尺规作图,保留作图痕迹,不写作法),并求出四边形CGEF周长的最小值.
①作点B关于直线m的对称点B′;②连接AB′,与直线m的交点P,则点P为所求线段AB′的长度即为AP+BP的最小值.
请你参考小明的做法解决下列问题:

(1)如图b,在等边△ABC中,AB=2,点E是AB的中点,AD是高,在AD上作出点P.(尺规作图,保留作图痕迹,不写作法),使得BP+PE的值最小,并求出最小值;
(2)如图c,在矩形ABCD中,AB=4,BC=6,G为边AD的中点,若E,F为边AB上的两个动点,点E在点F左侧,且EF=1,当四边形CGEF的周长最小时,请你在图c中确定点E,F的位置(尺规作图,保留作图痕迹,不写作法),并求出四边形CGEF周长的最小值.
考点:轴对称-最短路线问题
专题:
分析:(1)利用轴对称作出E点对称点E′,连接E′B即可得出P点坐标,要求BP+PE的值最小值,利用已知由勾股定理求出即可;
(2)利用已知可以得出GC,EF长度不变,求出GE+CF最小时即可得出四边形CGEF周长的最小值,利用轴对称得出E,F位置,即可求出.
(2)利用已知可以得出GC,EF长度不变,求出GE+CF最小时即可得出四边形CGEF周长的最小值,利用轴对称得出E,F位置,即可求出.
解答:解:(1)如图b,作E点关于AD的对称点E′,连接BE′,交AD于点P,连接EP,
∵在等边△ABC中,AB=2,点E是AB的中点,AD是高,
∴E′为AC的中点,
∴BE′⊥AC,
BE′=EP+BP=
=
=
;
 (2)如图c,作G关于AB的对称点M,
(2)如图c,作G关于AB的对称点M,
在CD上截取CH=1,然后连接HM交AB于E,
在EB上截取EF=1,
那么E、F两点即可满足使四边形CGEF的周长最小.
∵AB=4,BC=6,G为边AD的中点,
∴DG=AG=AM=3,
∵AE∥DH,
∴
=
,
∴
=
,
=
,
故AE=1,
∴GE=
=
,
BF=2,CF=
=
=2
,
CG=
=5,
∴C四边形GEFC=GE+EF+FC+CG=6+3
.
∵在等边△ABC中,AB=2,点E是AB的中点,AD是高,
∴E′为AC的中点,
∴BE′⊥AC,
BE′=EP+BP=
| BC2-E′C2 |
| 22-12 |
| 3 |
 (2)如图c,作G关于AB的对称点M,
(2)如图c,作G关于AB的对称点M,在CD上截取CH=1,然后连接HM交AB于E,
在EB上截取EF=1,
那么E、F两点即可满足使四边形CGEF的周长最小.
∵AB=4,BC=6,G为边AD的中点,
∴DG=AG=AM=3,
∵AE∥DH,
∴
| AE |
| DH |
| AM |
| DM |
∴
| AE |
| CD-HC |
| 1 |
| 3 |
| AE |
| 3 |
| 1 |
| 3 |
故AE=1,
∴GE=
| 12+32 |
| 10 |
BF=2,CF=
| BF2+BC2 |
| 22+62 |
| 10 |
CG=
| DC2+DG2 |
∴C四边形GEFC=GE+EF+FC+CG=6+3
| 10 |
点评:此题主要考查了利用轴对称求最短路径问题以及勾股定理等知识,利用GE+CF最小时即可得出四边形CGEF周长的最小值得出E,F位置是解题关键.

练习册系列答案
相关题目
不等式组
的解集是( )
|
| A、x>-1 | B、x>2 |
| C、-1<x<2 | D、x<2 |
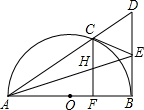 已知:C是以AB为直径的半圆O上一点,CF⊥AB于点F,直线AC与过B点的切线相交于点D,E为BD中点,连接AE交CF于点H,连接CE.
已知:C是以AB为直径的半圆O上一点,CF⊥AB于点F,直线AC与过B点的切线相交于点D,E为BD中点,连接AE交CF于点H,连接CE.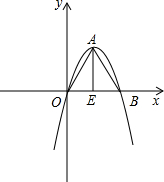 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”. 四边形ABCD是平行四边形,且AB=BE,CD=DF.
四边形ABCD是平行四边形,且AB=BE,CD=DF.