题目内容
15. 如图,在四边形ABCD中,∠A=∠C=90°.
如图,在四边形ABCD中,∠A=∠C=90°.(1)用直尺和圆规作⊙O,使它经过点A,B,D;
(2)检验点C是否在⊙O上,并说明理由.
分析 (1)连结BD,根据圆周角定理可判断BD为△ABD外接圆的直径,所以作BD的垂直平分线得到BD的中点O,再以O为圆心,OB为半径作⊙O即可;
(2)连结OC,如图,由∠BAD=90°得到BD为⊙O的直径,再由OC为斜边BD上的中线得到OC=OB=OD,于是可判断点C在⊙O上.
解答 解:(1)如图,⊙O为所作;
(2)点C在⊙O上.理由如下:
连结OC,如图,
∵⊙O为△BDA的外接圆,
而∠BAD=90°,
∴BD为⊙O的直径,
∵点O为BD的中点,∠BCD=90°,
∴OC为斜边BD上的中线,
∴OC=OB=OD,
∴点C在⊙O上.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
相关题目
3. 如图,a∥b,AB⊥a,BC交于b于E,若∠1=47°,则∠2的度数是( )
如图,a∥b,AB⊥a,BC交于b于E,若∠1=47°,则∠2的度数是( )
 如图,a∥b,AB⊥a,BC交于b于E,若∠1=47°,则∠2的度数是( )
如图,a∥b,AB⊥a,BC交于b于E,若∠1=47°,则∠2的度数是( )| A. | 137° | B. | 133° | C. | 120° | D. | 100° |
20. 把两块三角板按如图所示拼在一起,∠BOC=58°,则∠AOD的大小是( )
把两块三角板按如图所示拼在一起,∠BOC=58°,则∠AOD的大小是( )
 把两块三角板按如图所示拼在一起,∠BOC=58°,则∠AOD的大小是( )
把两块三角板按如图所示拼在一起,∠BOC=58°,则∠AOD的大小是( )| A. | 90° | B. | 100° | C. | 120° | D. | 122° |
7.如果$\sqrt{3a+12}$是二次根式,那么a的取值范围是( )
| A. | a≥-4 | B. | a≤-4 | C. | a≠-4 | D. | a>4 |
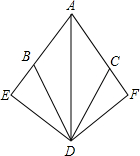 已知如图,BD=CD,∠ADB=∠ADC,DE、DF分别垂直于AB是AC交延长线于E、F.试问BE=CF吗?请说明理由.
已知如图,BD=CD,∠ADB=∠ADC,DE、DF分别垂直于AB是AC交延长线于E、F.试问BE=CF吗?请说明理由.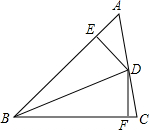 如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC垂足分别为E、F.
如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC垂足分别为E、F.