题目内容
7.如果$\sqrt{3a+12}$是二次根式,那么a的取值范围是( )| A. | a≥-4 | B. | a≤-4 | C. | a≠-4 | D. | a>4 |
分析 根据二次根式的性质和分式的意义,被开方数大于或等于0,可以求出a的范围.
解答 解:由$\sqrt{3a+12}$是二次根式,则3a+12≥0,
解得:a≥-4,
那么a的取值范围是:a≥-4.
故选:A.
点评 本题考查了二次根式有意义的条件,函数自变量的范围一般从三个方面考虑:当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数非负.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
18.某青年排球队10名队员的年龄如下:20,20,18,19,19,19,21,21,22,22,该队队员年龄的众数与中位数分别是( )
| A. | 20岁,19岁 | B. | 19岁,19岁 | C. | 19岁,20.5岁 | D. | 19岁,20岁 |
19.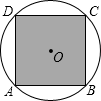 如图,正方形ABCD内接于⊙O,⊙O的直径为$\sqrt{2}$分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
如图,正方形ABCD内接于⊙O,⊙O的直径为$\sqrt{2}$分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
 如图,正方形ABCD内接于⊙O,⊙O的直径为$\sqrt{2}$分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
如图,正方形ABCD内接于⊙O,⊙O的直径为$\sqrt{2}$分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )| A. | $\frac{2}{π}$ | B. | $\frac{π}{2}$ | C. | $\frac{1}{2π}$ | D. | $\sqrt{2}π$ |
 如图,A,B两处是我国在南海上的两个观测站,从A处发现它的北偏西30°方向有一艘轮船,同时,从B处发现这艘轮船在它的北偏西60°方向.
如图,A,B两处是我国在南海上的两个观测站,从A处发现它的北偏西30°方向有一艘轮船,同时,从B处发现这艘轮船在它的北偏西60°方向. 如图,在四边形ABCD中,∠A=∠C=90°.
如图,在四边形ABCD中,∠A=∠C=90°.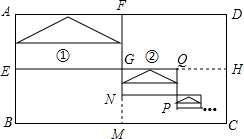 如图,在矩形ABCD中,AD=4,AB=2,连接其对边中点,得到四个矩形,顺次连接AF、FG、AE三边的中点,得到三角形①;连接矩形GMCH对边的中点,又得到四个矩形,顺次连接GQ、QP、GN三边的中点,得到三角形②;…;如此操作下去,得到三角形
如图,在矩形ABCD中,AD=4,AB=2,连接其对边中点,得到四个矩形,顺次连接AF、FG、AE三边的中点,得到三角形①;连接矩形GMCH对边的中点,又得到四个矩形,顺次连接GQ、QP、GN三边的中点,得到三角形②;…;如此操作下去,得到三角形 ,则三角形
,则三角形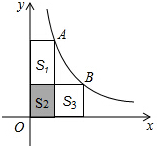 如图,A、B两点在反比例函数y=$\frac{4}{x}$的图象上,分别过A、B两点向坐标轴作垂线段,已知S2的面积为1,则S1+S3的面积为( )
如图,A、B两点在反比例函数y=$\frac{4}{x}$的图象上,分别过A、B两点向坐标轴作垂线段,已知S2的面积为1,则S1+S3的面积为( )