如图.?ABCD中.E为BC边上一点.以AE为边作正方形AEFG.若∠BAE=40°.∠CEF=15°.则∠D的度数是( )A．65°B．55°C．70°D．75° 题目和参考答案——青夏教育精英家教网—

题目内容

5．

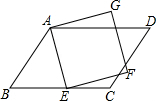如图，?ABCD中，E为BC边上一点，以AE为边作正方形AEFG，若∠BAE=40°，∠CEF=15°，则∠D的度数是（　　）

A．

65°

B．

55°

C．

70°

D．

75°

分析想办法求出∠B，利用平行四边形的性质∠D=∠B即可解决问题．

解答解：∵四边形ABCD是正方形，
∴∠AEF=90°，
∵∠CEF=15°，
∴∠AEB=180°-90°-15°=75°，
∵∠B=180°-∠BAE-∠AEB=180°-40°-75°=65°，
∵四边形ABCD是平行四边形，
∴∠D=∠B=65°
故选A．

点评本题考查正方形的性质、平行四边形的性质、三角形内角和定理等知识，解题的关键是灵活运用所学知识解决问题，学会用转化的思想思考问题，属于中考常考题型．

练习册系列答案

相关题目

15．

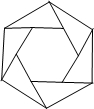如图，把正六边形各边按同一方向延长，使延长的线段与原正六边形的边长相等，顺次连接这六条线段外端点可以得到一个新的正六边形，…，重复上述过程，经过2018次后，所得到的正六边形边长是原正六边形边长的（　　）

（$\sqrt{2}$）²⁰¹⁶倍

（$\sqrt{3}$）²⁰¹⁷倍

（$\sqrt{3}$）²⁰¹⁸倍

（$\sqrt{2}$）²⁰¹⁹倍

16．

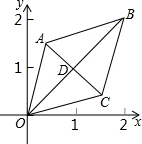如图，已知菱形OABC的顶点O（0，0），B（2，2），若菱形绕点O逆时针旋转，每秒旋转45°则第30秒时，菱形的对角线交点D的坐标为（　　）

（a³）²=a⁵

20．2022年将在北京--张家口举办冬季奥运会，北京将成为世界上第一个既举办夏季奥运会，又举办冬季奥运会的城市，某校开设了冰球选修课，12名同学被分成甲、乙两组进行训练，他们的身高（单位：cm）如表所示：

	队员1	队员2	队员3	队员4	队员5	队员6
甲组	176	177	175	176	177	175
乙组	178	175	170	174	183	176

设两队队员身高的平均数依次为$\overline{x}$_甲，$\overline{x}$_乙，方差依次为S_甲²，S_乙²，下列关系中正确的是（　　）

	A．	$\overline{x}$_甲=$\overline{x}$_乙，S_甲²＜S_乙²		B．	_{$\overline{x}$_甲=$\overline{x}$_乙，S_甲²＞S_乙²}
	C．	$\overline{x}$_甲＜$\overline{x}$_乙，S_甲²＜S_乙²		D．	$\overline{x}$_甲＞$\overline{x}$_乙，S_甲²＞S_乙²