题目内容
5.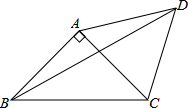 如图,等腰直角三角形ABC中,AB=AC,∠BAC=90°,∠BDC=45°.求证:AB=AD.
如图,等腰直角三角形ABC中,AB=AC,∠BAC=90°,∠BDC=45°.求证:AB=AD.
分析 以A为圆心,AB为半径作圆,根据∠BAC=90°,∠BDC=45°得到∠BDC=$\frac{1}{2}$∠BAC,从而得到点D在以A为圆心,以AB为半径的圆上,从而证得结论.
解答  证明:如图:以A为圆心,AB为半径作圆,
证明:如图:以A为圆心,AB为半径作圆,
∵AB=AC,
∴点C在⊙A上,
∵∠BAC=90°,∠BDC=45°,
∴∠BDC=$\frac{1}{2}$∠BAC,
∴点D在⊙A上,
∴AB=AD.
点评 本题考查了四点共圆的知识,解题的关键是能够根据题意作出以A为圆心,以AB为半径的圆,难度中等.

练习册系列答案
相关题目
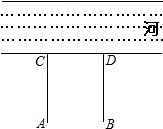 如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD.若A到河岸CD的中点的距离为500米.
如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD.若A到河岸CD的中点的距离为500米.