题目内容
13.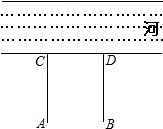 如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD.若A到河岸CD的中点的距离为500米.
如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD.若A到河岸CD的中点的距离为500米.(1)牧童从A处放牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短?用尺规作图在图中画出来.
(2)最短路程是多少?
分析 (1)如图,作点A关于河岸CD的对称点A′,连接A′B与CD相交于M,则牧童从A处把羊赶到河边饮水再回家,根据轴对称的性质和“两点之间线段最短”,连接A′B,得到最短距离为A′B,再根据相似三角形的性质得出CM=DM从而得出在CD的中点处饮水所走路程最短;
(2)根据A到河岸CD的中点的距离为500米,即可求出A'B的值.
解答 解:(1)作出A的对称点A′,连接A′B与CD相交于M,则牧童从A处把牛牵到河边饮水再回家,最短距离是A′B的长.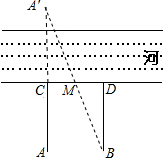
易得△A′CM∽△BDM,
因为AC=BD,所以A′C=BD,则$\frac{A′C}{BD}$=$\frac{CM}{MD}$,
所以CM=DM,M为CD的中点,
所以牧童从A处放牛牵到河边饮水后再回家,在CD的中点处饮水,所走路程最短
(2)因为A到河岸CD的中点的距离为500米,
所以A′到M的距离为500米,
所以A′B=1000米.
故最短距离是1000米.
点评 此题考查了轴对称的性质和“两点之间线段最短”,解答时要注意应用相似三角形的性质.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
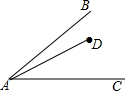 如图,∠BAC=30°,点D在∠BAC的内部,且AD=4cm,请在边AB和AC上确定一点M和N,使得△DMN的周长最小,并求这个最小值.
如图,∠BAC=30°,点D在∠BAC的内部,且AD=4cm,请在边AB和AC上确定一点M和N,使得△DMN的周长最小,并求这个最小值. 如图,一次函数的图象经过点A(0,2)、B(2,-2),写出这个函数的表达式.
如图,一次函数的图象经过点A(0,2)、B(2,-2),写出这个函数的表达式.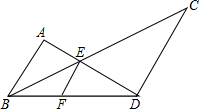 如图,F在BD上,BC、AD相交于点E,且AB∥CD∥EF,
如图,F在BD上,BC、AD相交于点E,且AB∥CD∥EF,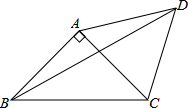 如图,等腰直角三角形ABC中,AB=AC,∠BAC=90°,∠BDC=45°.求证:AB=AD.
如图,等腰直角三角形ABC中,AB=AC,∠BAC=90°,∠BDC=45°.求证:AB=AD.