题目内容
14.化简:(1)$\sqrt{48}$
(2)$\sqrt{\frac{1}{3}}$
(3)$(\sqrt{3}-\sqrt{2})(\sqrt{2}+\sqrt{3})$.
分析 (1)、(2)利用二次根式的性质把二次根式化为最简二次根式;
(3)根据平方差公式计算.
解答 解:(1)原式=4$\sqrt{3}$;
(2)原式=$\frac{\sqrt{3}}{3}$;
(3)原式=($\sqrt{3}$-$\sqrt{2}$)($\sqrt{3}$+$\sqrt{2}$)
=3-2
=1.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
4.下列汽车标志图案,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,一次函数的图象经过点A(0,2)、B(2,-2),写出这个函数的表达式.
如图,一次函数的图象经过点A(0,2)、B(2,-2),写出这个函数的表达式.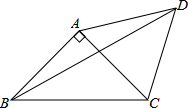 如图,等腰直角三角形ABC中,AB=AC,∠BAC=90°,∠BDC=45°.求证:AB=AD.
如图,等腰直角三角形ABC中,AB=AC,∠BAC=90°,∠BDC=45°.求证:AB=AD.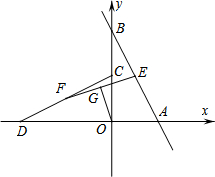 如图,直线y=mx-4m(m<0)与x,y轴分别相交于A,B两点,将△AOB绕点O逆时针转90°得到△COD,E为AB中点,F为CD中点,连接EF,G为EF中点,连接OG.若OG=$\sqrt{10}$,则m的值为-2.
如图,直线y=mx-4m(m<0)与x,y轴分别相交于A,B两点,将△AOB绕点O逆时针转90°得到△COD,E为AB中点,F为CD中点,连接EF,G为EF中点,连接OG.若OG=$\sqrt{10}$,则m的值为-2.