Question

7．如图，已知在梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，AB=8cm，BC=26cm，动点P从A点开始沿AD边以1cm/s的速度向D运动，动点Q从C点开始沿CB边以3cm/s的速度向B运动，P、Q分别从A、C同时出发，当其中一点到端点时，另一点也随之停止运动，设运动时间为t秒，当t为何值时，线段PQ=CD．

Answer 1

分析 首先过点D作DE⊥BC于点E，过点P作PF⊥BC于点F，易得四边形ABED、四边形ABFP都是矩形，然后可求得CD的长，用t表示出PQ，即可得方程：64+（26-4t）²=68，解此方程即可求得答案．

解答 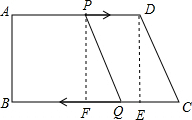解：过点D作DE⊥BC于点E，过点P作PF⊥BC于点F，
根据题意得：AP=tcm，CQ=3tcm，
∵在梯形ABCD中，AD∥BC，∠B=90°，
∴四边形ABED、四边形ABFP都是矩形，
∵AD=24cm，AB=8cm，BC=26cm，
∴BE=AD=24cm，PF=DE=AB=8cm，
∴CE=BC-BE=2cm，
∴CD²=CE²+DE²=68cm²，
∵FQ=BC-CQ-BF=BC-CQ-AP=26-t-2t=26-4t（cm），
∴PQ²=PF²+FQ²=64+（26-4t）²，
∴当64+（26-4t）²=68时，线段PQ=CD，
解得：t=6或t=7．
∴当t为6或7时，线段PQ=CD．

点评 此题考查了梯形的性质、勾股定理以及矩形的判定与性质．注意准确作出辅助线是解此题的关键．