题目内容
1.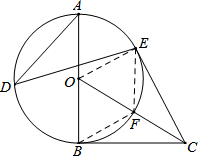 如图,以Rt△OBC的直角边OB为半径作⊙O,点D、E都在⊙O上,且∠ADE=∠OCB,连接CE.
如图,以Rt△OBC的直角边OB为半径作⊙O,点D、E都在⊙O上,且∠ADE=∠OCB,连接CE.(1)求证:CE为⊙O的切线.
(2)线段CO与⊙O交于点F,若F点为CO的中点,连接EO、EF、BF,试判断四边形BOEF的形状.
分析 (1)连接OE,根据圆周角定理得到∠AOE=2∠D,得到∠AOE=2∠BCO,根据三角形的内角和得到∠BCO+∠BOC=90°,推出∠BOC=∠EOC,根据全等三角形的性质得到∠OEC=∠OBC=90°,即可得到结论;
(2)根据直角三角形的性质得到EF=BF=OF,由于OB=OE=OF.等量代换得到OB=OE=EF=BF,于是得到结论.
解答 (1)证明:连接OE,
∴∠AOE=2∠D,
∵∠D=∠BCO,
∴∠AOE=2∠BCO,
∵∠OBC=90°,
∴∠BCO+∠BOC=90°,
∴2∠BCO+2∠BOC=180°,
∴∠AOE+2∠BOC=180°,
∵∠AOE+∠EOC+∠BOC=180°,
∴∠BOC=∠EOC,
在△BOC与△EOC中,$\left\{\begin{array}{l}{OB=OE}\\{∠BOC=∠EOC}\\{OC=OC}\end{array}\right.$,
∴△BDO≌△EOC,
∴∠OEC=∠OBC=90°,
∴OE⊥CE,
∴CE为⊙O的切线;
(2)解:∵∠OBC=∠OEC=90°,F点为CO的中点,
∴EF=BF=OF,
∵OB=0E=OF.
∴OB=OE=EF=BF,
∴四边形BOEF是菱形.
点评 本题考查了切线的判定,全等三角形的判断和性质,菱形的判定,直角三角形的性质,正确的识别图形是解题的关键.

练习册系列答案
相关题目
16.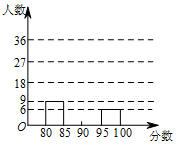 为活跃校园生活,某校开展了“我歌唱我快乐”海选比赛活动,抽取海选中部分参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如下:
为活跃校园生活,某校开展了“我歌唱我快乐”海选比赛活动,抽取海选中部分参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如下:
(1)请在图中补全频数分布直方图;
(2)抽取的这部分参赛同学成绩的中位数落在哪个分数段?
(3)如果该校参加人数1000人,请估计分数在95≤x<100段的人数约为多少?
 为活跃校园生活,某校开展了“我歌唱我快乐”海选比赛活动,抽取海选中部分参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如下:
为活跃校园生活,某校开展了“我歌唱我快乐”海选比赛活动,抽取海选中部分参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如下:| 分数段 | 频数 | 频率 |
| 80≤x<85 | 9 | 0.15 |
| 85≤x<90 | m | 0.45 |
| 90≤x<95 | ■ | ■ |
| 95≤x<100 | 6 | n |
(2)抽取的这部分参赛同学成绩的中位数落在哪个分数段?
(3)如果该校参加人数1000人,请估计分数在95≤x<100段的人数约为多少?
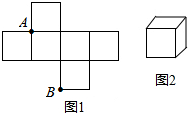 如图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,一个蚂蚁在图1中的A点,围成图2后,蚂蚁从A点开始沿正方体的棱爬行,求爬到B点的最短距离是多少?
如图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,一个蚂蚁在图1中的A点,围成图2后,蚂蚁从A点开始沿正方体的棱爬行,求爬到B点的最短距离是多少?