题目内容
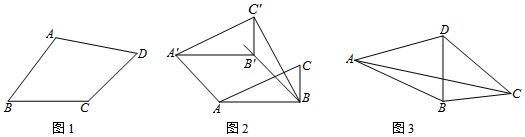
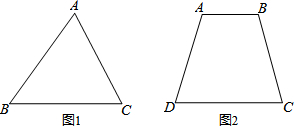
9.类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.(1)概念理解:如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.
(2)问题探究:如图2,小红画了一个 Rt△ABC,其中∠ABC=90°,AB=2,BC=1,并将 Rt△ABC沿∠ABC的平分线BB'方向平移得到△A'B'C',连结AA',BC',小红要使平移后的四边形ABC'A'是“等邻边四边形”,应平移多少距离(即线段BB'的长)?
(3)拓展应用:如图3“等邻边四边形”ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,AC=$\sqrt{2}$AB,试探究BC,CD,BD的数量关系.
分析 (1)由“等邻边四边形”的定义易得出结论;
(2)①先利用平行四边形的判定定理得平行四边形,再利用“等邻边四边形”定义得邻边相等,得出结论;
②由平移的性质易得BB′=AA′,A′B′∥AB,A′B′=AB=2,B′C′=BC=1,A′C′=AC=$\sqrt{5}$,再利用“等邻边四边形”定义分类讨论,由勾股定理得出结论;
(3)由旋转的性质可得△ABF≌△ADC,由全等性质得∠ABF=∠ADC,∠BAF=∠DAC,AF=AC,FB=CD,利用相似三角形判定得△ACF∽△ABD,由相似的性质和四边形内角和得∠CBF=90°,利用勾股定理,等量代换得出结论.
解答 解:(1)AB=BC或BC=CD或CD=AD或AD=AB(任写一个即可);
(2)①正确,理由为: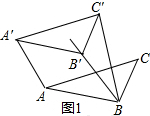
∵四边形的对角线互相平分,
∴这个四边形是平行四边形,
∵四边形是“等邻边四边形”,
∴这个四边形有一组邻边相等,
∴这个“等邻边四边形”是菱形;
②∵∠ABC=90°,AB=2,BC=1,
∴AC=$\sqrt{5}$,
∵将Rt△ABC平移得到△A′B′C′,
∴BB′=AA′,A′B′∥AB,A′B′=AB=2,B′C′=BC=1,A′C′=AC=$\sqrt{5}$,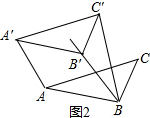
(I)如图1,当AA′=AB时,BB′=AA′=AB=2;
(II)如图2,当AA′=A′C′时,BB′=AA′=A′C′=$\sqrt{5}$;
(III)当A′C′=BC′=$\sqrt{5}$时,
如图3,延长C′B′交AB于点D,则C′B′⊥AB,
∵BB′平分∠ABC,
∴∠ABB′=$\frac{1}{2}$∠ABC=45°,
∴∠BB′D=′∠ABB′=45°
∴B′D=B,
设B′D=BD=x,
则C′D=x+1,BB′=$\sqrt{2}$x,
∵在Rt△BC′D中,BD2+(C′D)2=(BC′)2
∴x2+(x+1)2=($\sqrt{5}$)2,
解得:x1=1,x2=-2(不合题意,舍去),
∴BB′=$\sqrt{2}$x=$\sqrt{2}$
(Ⅳ)当BC′=AB=2时,
如图4,与(Ⅲ)方法一同理可得:BD2+(C′D)2=(BC′)2,
设B′D=BD=x,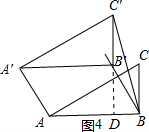
则x2+(x+1)2=22,
解得:x1=$\frac{-1+\sqrt{7}}{2}$,x2=$\frac{-1-\sqrt{7}}{2}$(不合题意,舍去),
∴BB′=$\sqrt{2}$x=$\frac{\sqrt{14}-\sqrt{2}}{2}$;
(3)BC,CD,BD的数量关系为:BC2+CD2=2BD2,
如图5,
∵AB=AD,
∴将△ADC绕点A旋转到△ABF,连接CF,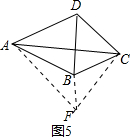
∴△ABF≌△ADC,
∴∠ABF=∠ADC,∠BAF=∠DAC,AF=AC,FB=CD,
∴∠BAD=∠CAF,$\frac{AC}{AF}$=$\frac{AD}{AB}$=1,
∴△ACF∽△ABD,
∴$\frac{CF}{BD}$=$\frac{AC}{AB}$=$\frac{\sqrt{2}}{2}$,
∴CF=$\sqrt{2}$BD,
∵∠BAD+∠ADC+∠BCD+∠ABC=360°,
∴∠ABC+∠ADC-360°-(∠BAD+∠BCD)=360°-90°=270°,
∴∠ABC+∠ABF=270°,
∴∠CBF=90°,
∴BC2+FB2=CF2=($\sqrt{2}$BD)2=2BD2,
∴BC2+CD2=2BD2.
点评 此题属于四边形的综合题.属于新定义题目,考查了菱形的判定,勾股定理,相似三角形的性质等知识.注意理解新定义,分类讨论是解答此题的关键.

| A. | a2•a3=a6 | B. | a3÷a=a3 | C. | (a2)3=a6 | D. | (3a3)3=9a9 |
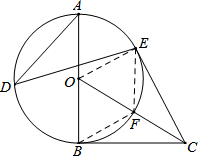 如图,以Rt△OBC的直角边OB为半径作⊙O,点D、E都在⊙O上,且∠ADE=∠OCB,连接CE.
如图,以Rt△OBC的直角边OB为半径作⊙O,点D、E都在⊙O上,且∠ADE=∠OCB,连接CE. 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-2),B(3,-1),C(1,-1).
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-2),B(3,-1),C(1,-1).