题目内容
20.(1)计算:$\sqrt{8}$+|2$\sqrt{2}$-3|-($\frac{1}{3}$)-1-(2016+$\sqrt{2}$)0;(2)求下列方程中的x:
①(x-1)2=49;
②-8(1-x)3=27.
分析 (1)本题涉及零指数幂、负整数指数幂、二次根式化简、绝对值四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
(2)①开平方得出(x-1)的值,继而可得出x的值.
②两边开立方,即可得出一个一元一次方程,求出即可.
解答 (1)解:$\sqrt{8}$+|2$\sqrt{2}$-3|-($\frac{1}{3}$)-1-(2016+$\sqrt{2}$)0;
=2$\sqrt{2}$+3-2$\sqrt{2}$-3-1
=-1;
(2)解:①(x-1)2=49
开平方得:x-1=±7,
解得:x=8或-6.
②-8(1-x)3=27
(1-x)3=-$\frac{27}{8}$,
1-x=-$\frac{3}{2}$,
x=$\frac{5}{2}$.
点评 本题考查了考查实数的综合运算能力以及立方根和平方根的应用,熟练掌握零指数幂、负整数指数幂、二次根式、绝对值等的运算是本题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
8. 如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆半径的$\sqrt{2}$倍,为了使航船(S)不进入暗礁区,那么S 对两灯塔A,B的视角∠ASB必须( )
如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆半径的$\sqrt{2}$倍,为了使航船(S)不进入暗礁区,那么S 对两灯塔A,B的视角∠ASB必须( )
 如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆半径的$\sqrt{2}$倍,为了使航船(S)不进入暗礁区,那么S 对两灯塔A,B的视角∠ASB必须( )
如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆半径的$\sqrt{2}$倍,为了使航船(S)不进入暗礁区,那么S 对两灯塔A,B的视角∠ASB必须( )| A. | 大于60° | B. | 小于60° | C. | 大于45° | D. | 小于45° |
5.一架5m长的梯子斜靠在一竖直的墙上,这时梯脚距离墙角3m,如果梯子的顶端沿墙下滑1m,那么梯脚移动的距离是( )
| A. | 0.5m | B. | 0.8m | C. | 1m | D. | 1.2m |
 如图,在Rt△ABC中,∠B=90°,∠ACB=45°,∠D=30°,B、C、D在同一直线上,连接AD,若AB=$\sqrt{3}$,则sin∠CAD=$\frac{\sqrt{6}-\sqrt{2}}{4}$.
如图,在Rt△ABC中,∠B=90°,∠ACB=45°,∠D=30°,B、C、D在同一直线上,连接AD,若AB=$\sqrt{3}$,则sin∠CAD=$\frac{\sqrt{6}-\sqrt{2}}{4}$.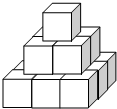 如图,几个棱长为1的小正方体在地板上堆积成一个模型,表面喷涂红色染料,那么染有红色染料的模型的表面积为42.
如图,几个棱长为1的小正方体在地板上堆积成一个模型,表面喷涂红色染料,那么染有红色染料的模型的表面积为42. 如图,AB是⊙O的一条弦,M,N是⊙O上两个动点,且在弦AB的异侧,若∠AMB=45°,若四边形MANB面积的最大值是4$\sqrt{2}$,则⊙O的半径为2.
如图,AB是⊙O的一条弦,M,N是⊙O上两个动点,且在弦AB的异侧,若∠AMB=45°,若四边形MANB面积的最大值是4$\sqrt{2}$,则⊙O的半径为2.