题目内容
10. 如图,AB是⊙O的一条弦,M,N是⊙O上两个动点,且在弦AB的异侧,若∠AMB=45°,若四边形MANB面积的最大值是4$\sqrt{2}$,则⊙O的半径为2.
如图,AB是⊙O的一条弦,M,N是⊙O上两个动点,且在弦AB的异侧,若∠AMB=45°,若四边形MANB面积的最大值是4$\sqrt{2}$,则⊙O的半径为2.
分析 过点O作OC⊥AB于C,交⊙O于D、E两点,连结OA、OB、DA、DB、EA、EB,根据圆周角定理得∠AOB=2∠AMB=90°,则△OAB为等腰直角三角形,所以AB=$\sqrt{2}$OA,由于S四边形MANB=S△MAB+S△NAB,而当M点到AB的距离最大,△MAB的面积最大;当N点到AB的距离最大时,△NAB的面积最大,即M点运动到D点,N点运动到E点,所以四边形MANB面积的最大值=S四边形DAEB=$\frac{1}{2}$AB×DE,求出OA即可.
解答 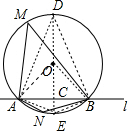 解:过点O作OC⊥AB于C,交⊙O于D、E两点,连结OA、OB、DA、DB、EA、EB,如图,
解:过点O作OC⊥AB于C,交⊙O于D、E两点,连结OA、OB、DA、DB、EA、EB,如图,
∵∠AMB=45°,
∴∠AOB=2∠AMB=90°,
∴△OAB为等腰直角三角形,
∴AB=$\sqrt{2}$OA,
∵S四边形MANB=S△MAB+S△NAB,
∴当M点到AB的距离最大,△MAB的面积最大;当N点到AB的距离最大时,△NAB的面积最大,
即M点运动到D点,N点运动到E点,
此时四边形MANB面积的最大值=S四边形DAEB=$\frac{1}{2}$AB×DE=4$\sqrt{2}$,
∴$\frac{1}{2}$×$\sqrt{2}$OA×2OA=4$\sqrt{2}$,
解得:OA=2,即⊙O的半径为2;
故答案为:2.
点评 本题考查了垂径定理、圆周角定理、等腰直角三角形的判定与性质、四边形面积的计算;熟练掌握垂径定理和圆周角定理,得出四边形MANB面积取最大值时M点运动到D点,N点运动到E点是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.将平面直角坐标系内某图形上各个点的纵坐标都乘以-1,横坐标不变,所得图形与原图形的关系是( )
| A. | 关于y轴对称 | B. | 关于x轴对称 | ||
| C. | 沿x轴向左平移1个单位长度 | D. | 沿y轴向下平移1个单位长度 |
19.据统计,第十三届中国•四川光雾山红叶节实现旅游收入约为14.36亿元,则近似数14.36亿元精确到( )
| A. | 百分位 | B. | 百万位 | C. | 千万位 | D. | 0.01 |
 如图,一直线BC与已知直线AB:y=2x+1关于y轴对称.
如图,一直线BC与已知直线AB:y=2x+1关于y轴对称. 如图,大圆的半径是R,小圆的面积是大圆面积的$\frac{2}{3}$,当R=3时,求圆环(阴影部分)的面积.
如图,大圆的半径是R,小圆的面积是大圆面积的$\frac{2}{3}$,当R=3时,求圆环(阴影部分)的面积.