题目内容
8. 如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆半径的$\sqrt{2}$倍,为了使航船(S)不进入暗礁区,那么S 对两灯塔A,B的视角∠ASB必须( )
如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆半径的$\sqrt{2}$倍,为了使航船(S)不进入暗礁区,那么S 对两灯塔A,B的视角∠ASB必须( )| A. | 大于60° | B. | 小于60° | C. | 大于45° | D. | 小于45° |
分析 连接OA,OB,AB及BC,由AB等于圆半径的$\sqrt{2}$倍,得到三角形AOB为直角三角形,根据直角三角形的性质可得∠AOB=90°,由同弧所对的圆周角等于所对圆心角的一半,求出∠ACB的度数,再由∠ACB为△SCB的外角,根据三角形的外角性质:三角形的外角大于与它不相邻的任意一个内角,可得∠ASB小于∠ACB,即可得到正确的选项.
解答 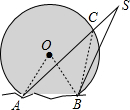 解:连接OA,OB,AB,BC,如图所示:
解:连接OA,OB,AB,BC,如图所示:
∵AO=BO,AB=$\sqrt{2}$AO,
∴△AOB为直角三角形,
∴∠AOB=90°,
∵∠ACB与∠AOB所对的弧都为$\widehat{AB}$,
∴∠ACB=$\frac{1}{2}$∠AOB=45°,
又∠ACB为△SCB的外角,
∴∠ACB>∠ASB,即∠ASB<45°.
故选D.
点评 此题考查了圆周角定理,三角形的外角性质,以及直角三角形的性质,根据题意作出辅助线,灵活运用圆周角定理是解本题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 如图,抛物线y=x2+bx+c(c>0)与y轴交于点C,顶点为A,抛物线的对称轴交x轴于点E,交BC于点D,tan∠AOE=$\frac{3}{2}$.直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是$\frac{9}{2}$或$\frac{27}{2}$.
如图,抛物线y=x2+bx+c(c>0)与y轴交于点C,顶点为A,抛物线的对称轴交x轴于点E,交BC于点D,tan∠AOE=$\frac{3}{2}$.直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是$\frac{9}{2}$或$\frac{27}{2}$. 如图,已知两条线段a、b(a>b)
如图,已知两条线段a、b(a>b)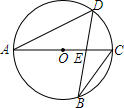 如图,AC是⊙O的直径,AC=10,弦BD交AC于点E.
如图,AC是⊙O的直径,AC=10,弦BD交AC于点E. 如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.
如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.