题目内容
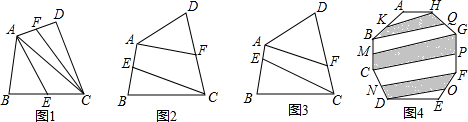
7.我们知道,三角形的中线平分三角形的面积.(1)AE 是△AEC的中线.在△ABC的外部作△ACD,F是AD的中点,连接CF(图1),若四边形ABCD的面积是S,则四边形AECF的面积是$\frac{S}{2}$.
(2)任意四边形ABCD的面积是S,E、F分别是一组对边AB、CD的中点,连接AF、CE(图2),则四边形AECF的面积是$\frac{S}{2}$.
(3)四边形ABCD的面积是10,E,F分别是一组对边AB,CD上的点,且AE=$\frac{1}{3}$AB,CF=$\frac{1}{3}$CD,连接AF,CE(图3),则四边形AECF的面积是$\frac{10}{3}$.
(4)若八边形ABCDEFGH的面积是10,K,M,N,O,P,Q分别是AB,BC,CD,EF,FG,GH的中点,连接KH,MG,NF,OD,PC,QB(图4),则图中阴影部分的面积是5.
分析 (1)分别可得S△AEC=$\frac{1}{2}$S△ABC,S△AFC=$\frac{1}{2}$S△ACD,从而可得S四边形AECF=$\frac{1}{2}$S四边形ABCD.
(2)同(1),可得S四边形AECF=$\frac{1}{2}$S四边形ABCD.
(3)分别得到S△AEC=$\frac{1}{3}$S△ABC,S△AFC=$\frac{1}{3}$S△ACD,从而可得S四边形AECF=$\frac{1}{3}$S四边形ABCD.
(4)连接CF、BG,根据(2)的结论,可得答案.
解答 解:(1)∵AE是△AEC的中线,
∴CE=$\frac{1}{2}$BC,
∴S△AEC=$\frac{1}{2}$S△ABC,
同理:S△AFC=$\frac{1}{2}$S△ACD,
∴S四边形AECF=$\frac{1}{2}$S四边形ABCD=$\frac{S}{2}$.
(2)连接AC,如图a: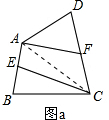
则S四边形AECF=$\frac{1}{2}$S四边形ABCD=$\frac{S}{2}$.
(3)连接AC,如图b: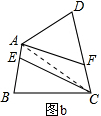
∵AE=$\frac{1}{3}$AB,CF=$\frac{1}{3}$CD,
∴S△AEC=$\frac{1}{3}$S△ABC,S△AFC=$\frac{1}{3}$S△ACD,
∴S四边形AECF=$\frac{1}{3}$S四边形ABCD=$\frac{10}{3}$.
(4)连接CF、BG,如图c: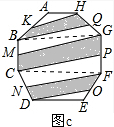
则可得S四边形KBQH=$\frac{1}{2}$S四边形ABGH,S四边形MCPG=$\frac{1}{2}$S四边形BCFG,S四边形NDOF=$\frac{1}{2}$S四边形CDEF,
∴S阴影=$\frac{1}{2}$S八边形ABCDEFGH=5.
故答案为:$\frac{S}{2}$、$\frac{S}{2}$、$\frac{10}{3}$、5.
点评 本题考查了四边形的综合,解答本题的关键是掌握三角形中线的性质,注意融会贯通,将前面的结论运用到后面的解题中去,难度一般.

 阅读快车系列答案
阅读快车系列答案| A. | 4$\sqrt{2}$-$\sqrt{6}$ | B. | 6-$\sqrt{2}$ | C. | 6-$\sqrt{6}$ | D. | 2$\sqrt{2}$ |
| A. | 28 | B. | 216 | C. | 216-1 | D. | 28-1 |
| A. |  | B. |  | C. |  | D. |  |