题目内容
11.在四边形ABCD中,AD∥BC,AB=8cm,AD=16cm,BC=22cm,∠AEC=90°.点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒.(1)当t=$\frac{11}{2}$时,四边形ABQP成为矩形?
(2)当t=4或$\frac{11}{2}$时,以点P、Q与点A、B、C、D中的任意两个点为顶点的四边形为平行四边形?
(3)四边形PBQD是否能成为菱形?若能,求出t的值;若不能,请说明理由,并探究如何改变Q点的速度(匀速运动),使四边形PBQD在某一时刻为菱形,求点Q的速度.

分析 (1)由∠B=90°,AP∥BQ,由矩形的判定可知当AP=BQ时,四边形ABQP成为矩形;
(2)由(1)可求得点P、Q与点A、B为顶点的四边形为平行四边形;然后由当PD=CQ时,CDPQ是平行四边形,求得t的值;
(3)由PD∥BQ,当PD=BQ=BP时,四边形PBQD能成为菱形,先由PD=BQ求出运动时间t的值,再代入求BP,发现BP≠PD,判断此时四边形PBQD不能成为菱形;设Q点的速度改变为vcm/s时,四边形PBQD在时刻t为菱形,根据PD=BQ=BP列出关于v、t的方程组,解方程组即可求出点Q的速度.
解答  解:(1)如图1,∵∠B=90°,AP∥BQ,
解:(1)如图1,∵∠B=90°,AP∥BQ,
∴当AP=BQ时,四边形ABQP成为矩形,
此时有t=22-3t,解得t=$\frac{11}{2}$.
∴当t=$\frac{11}{2}$时,四边形ABQP成为矩形;
故答案为:$\frac{11}{2}$; (2)如图1,当t=$\frac{11}{2}$时,四边形ABQP成为矩形,
(2)如图1,当t=$\frac{11}{2}$时,四边形ABQP成为矩形,
如图2,当PD∥CQ时,四边形CDPQ是平行四边形,
则16-t=3t,
解得:t=4,
∴当t=$\frac{11}{2}$或4时,以点P、Q与点A、B、C、D中的任意两个点为顶点的四边形为平行四边形;
故答案为:$\frac{11}{2}$或4;
(3)四边形PBQD不能成为菱形.理由如下:
∵PD∥BQ, ∴当PD=BQ=BP时,四边形PBQD能成为菱形.
∴当PD=BQ=BP时,四边形PBQD能成为菱形.
由PD=BQ,得16-t=22-3t,
解得:t=3,
当t=3时,PD=BQ=13,BP=$\sqrt{A{B}^{2}+A{P}^{2}}$=$\sqrt{{8}^{2}+{t}^{2}}$=$\sqrt{{8}^{2}+{3}^{2}}$=$\sqrt{73}$≠13,
∴四边形PBQD不能成为菱形;
如果Q点的速度改变为vcm/s时,能够使四边形PBQD在时刻ts为菱形,
由题意,得$\left\{\begin{array}{l}{16-t=22-vt}\\{16-t=\sqrt{{8}^{2}+{t}^{2}}}\end{array}\right.$,解得$\left\{\begin{array}{l}{t=6}\\{v=2}\end{array}\right.$.
故点Q的速度为2cm/s时,能够使四边形PBQD在某一时刻为菱形.
点评 此题属于四边形的综合题.考查了矩形的判定、菱形的判定以及勾股定理等知识.注意掌握分类讨论思想与方程思想的应用是解此题的关键.

| A. | 2$\sqrt{3}$ | B. | $2\sqrt{5}$ | C. | 2 | D. | $\sqrt{5}$ |
 如图,已知直线AB,CD相交于点O,OE平分∠AOD,FO⊥AB,垂足为O,若$\frac{3}{2}$∠BOD=∠DOE.
如图,已知直线AB,CD相交于点O,OE平分∠AOD,FO⊥AB,垂足为O,若$\frac{3}{2}$∠BOD=∠DOE.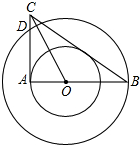 如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB. 如图,AP⊥AQ,半径为5 的⊙O于AP相切于点T,与AQ交于点B、C.
如图,AP⊥AQ,半径为5 的⊙O于AP相切于点T,与AQ交于点B、C. 如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O,求证:△ABC≌△DCB.
如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O,求证:△ABC≌△DCB. 如图,有大小两个同心圆,大圆的弦AB与小圆相切,若AB=8,则圆环(阴影部分)的面积是16π.(不取近似值)
如图,有大小两个同心圆,大圆的弦AB与小圆相切,若AB=8,则圆环(阴影部分)的面积是16π.(不取近似值)