题目内容
20．菱形的边长和一条对角线长都为2，则另一条对角线长为（ ）| A． | 2$\sqrt{3}$ | B． | $2\sqrt{5}$ | C． | 2 | D． | $\sqrt{5}$ |
分析 根据菱形的对角线互相垂直平分，得已知对角线的一半是1．根据勾股定理，得要求的对角线的一半是$\sqrt{3}$，则另一条对角线的长是2$\sqrt{3}$．
解答 解：如图：
在菱形ABCD中，AB=2，AC=2，
∵对角线互相垂直平分，
∴∠AOB=90°，AO=1，
在Rt△AOB中，BO=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$，
∴BD=2BO=2$\sqrt{3}$．
故选：A．
点评 本题考查了菱形的性质，注意掌握：菱形的对角线互相垂直平分，同时要熟练运用勾股定理．
练习册系列答案
口算题天天练系列答案
相关题目
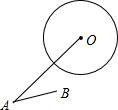如图，⊙O的半径为1，OA=2.5，∠OAB=30°，则AB与⊙O的位置关系是相离．