题目内容
3. 如图,有大小两个同心圆,大圆的弦AB与小圆相切,若AB=8,则圆环(阴影部分)的面积是16π.(不取近似值)
如图,有大小两个同心圆,大圆的弦AB与小圆相切,若AB=8,则圆环(阴影部分)的面积是16π.(不取近似值)
分析 设AB于小圆切于点C,连接OC,OB,利用垂径定理即可求得BC的长,根据圆环(阴影)的面积=π•OB2-π•OC2=π(OB2-OC2),以及勾股定理即可求解.
解答 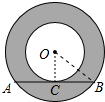 解:设AB于小圆切于点C,连接OC,OB.
解:设AB于小圆切于点C,连接OC,OB.
∵AB于小圆切于点C,
∴OC⊥AB,
∴BC=AC=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4.
∵圆环(阴影)的面积=π•OB2-π•OC2=π(OB2-OC2)
又∵直角△OBC中,OB2=OC2+BC2
∴圆环(阴影)的面积=π•OB2-π•OC2=π(OB2-OC2)=π•BC2=16π.
故答案是:16π.
点评 本题考查了垂径定理,切线的性质,以及勾股定理,解题的关键是正确作出辅助线,注意到圆环(阴影)的面积=π•OB2-π•OC2=π(OB2-OC2),利用勾股定理把圆的半径之间的关系转化为直角三角形的边的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.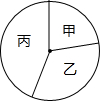 如图,将一个圆分割成甲、乙、丙三个扇形,使它们的圆心角的度数之比为2:3:4.若圆的半径为3,则扇形丙的面积为( )
如图,将一个圆分割成甲、乙、丙三个扇形,使它们的圆心角的度数之比为2:3:4.若圆的半径为3,则扇形丙的面积为( )
 如图,将一个圆分割成甲、乙、丙三个扇形,使它们的圆心角的度数之比为2:3:4.若圆的半径为3,则扇形丙的面积为( )
如图,将一个圆分割成甲、乙、丙三个扇形,使它们的圆心角的度数之比为2:3:4.若圆的半径为3,则扇形丙的面积为( )| A. | $\frac{2}{3}$π | B. | $\frac{4}{9}$π | C. | 3π | D. | 4π |
 如图,一圆柱高4m,底面周长为6m,现需按如图方式缠绕一圈彩带进行装饰,则彩带最短要用10m.
如图,一圆柱高4m,底面周长为6m,现需按如图方式缠绕一圈彩带进行装饰,则彩带最短要用10m.
 如图,等边△ABC的边长为2,P是BC边上的任一点(与B、C不重合),设BP=x,连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB、AC交于点M、N.
如图,等边△ABC的边长为2,P是BC边上的任一点(与B、C不重合),设BP=x,连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB、AC交于点M、N.