题目内容
1.有甲、乙、丙三种货物,若购甲3件,乙7件,丙1件,共需315元;若购甲4件,乙10件,丙1件,共需420元.现在购买甲、乙、丙各1件,共需( )| A. | 105元 | B. | 210元 | C. | 170元 | D. | 不能确定 |
分析 等量关系为:甲3件的总价+乙7件的总价+丙1件的总价=315,4件的总价+乙10件的总价+丙1件的总价=420,把相关数值代入,都整理为等式左边为x+y+z的等式,设法消去等号右边含未知数的项,可得甲、乙、丙各1件共需的费用.
解答 解:设购买甲、乙、丙各1件分别需要x,y,z元,则依题意
$\left\{\begin{array}{l}{3x+7y+z=315①}\\{4x+10y+z=420②}\end{array}\right.$,
由①×3-②×2得,x+y+z=105,
即现在购买甲、乙、丙各1件,共需105元.
故选:A.
点评 本题考查了三元一次方程组的应用;根据总价得到2个等量关系是解决本题的关键;难点是把2个等式整理为只含(x+y+z)的等式.

练习册系列答案
相关题目
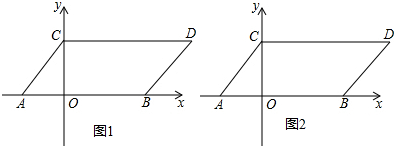
 如图,已知CD∥EF,CH∥AB,∠EFG+∠BCD=∠ABC,求证:AB∥GF.
如图,已知CD∥EF,CH∥AB,∠EFG+∠BCD=∠ABC,求证:AB∥GF.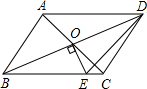 如图,平行四边形ABCD的对角线相交于点O,且DC≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为6cm,则平行四边形ABCD的周长为12cm.
如图,平行四边形ABCD的对角线相交于点O,且DC≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为6cm,则平行四边形ABCD的周长为12cm.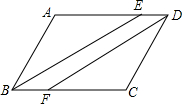 如图,四边形ABCD是平行四边形,BE平分∠ABC,DF平分∠ADC,求证:四边形DEBF是平行四边形.
如图,四边形ABCD是平行四边形,BE平分∠ABC,DF平分∠ADC,求证:四边形DEBF是平行四边形.