题目内容
13.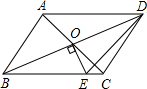 如图,平行四边形ABCD的对角线相交于点O,且DC≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为6cm,则平行四边形ABCD的周长为12cm.
如图,平行四边形ABCD的对角线相交于点O,且DC≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为6cm,则平行四边形ABCD的周长为12cm.
分析 由平行四边形的性质得出AB=CD,BC=AD,OB=OD,再根据线段垂直平分线的性质得出BE=DE,由△CDE的周长得出BC+CD=6cm,即可求出平行四边形ABCD的周长.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OB=OD,
∵OE⊥BD,
∴BE=DE,
∵△CDE的周长为6cm,
∴DE+CE+CD=BE+CE+CD=BC+CD=6cm,
∴平行四边形ABCD的周长=2(BC+CD)=12cm;
故答案为:12cm.
点评 本题考查了平行四边形的性质、线段垂直平分线的性质以及三角形、平行四边形周长的计算;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
1.有甲、乙、丙三种货物,若购甲3件,乙7件,丙1件,共需315元;若购甲4件,乙10件,丙1件,共需420元.现在购买甲、乙、丙各1件,共需( )
| A. | 105元 | B. | 210元 | C. | 170元 | D. | 不能确定 |
3.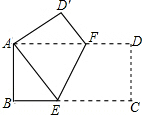 如图,在矩形ABCD中,AB=4,BC=8,将矩形ABCD沿EF折叠,使点C与A重合,则折痕EF的长为( )
如图,在矩形ABCD中,AB=4,BC=8,将矩形ABCD沿EF折叠,使点C与A重合,则折痕EF的长为( )
 如图,在矩形ABCD中,AB=4,BC=8,将矩形ABCD沿EF折叠,使点C与A重合,则折痕EF的长为( )
如图,在矩形ABCD中,AB=4,BC=8,将矩形ABCD沿EF折叠,使点C与A重合,则折痕EF的长为( )| A. | 5 | B. | 6 | C. | 5$\sqrt{2}$ | D. | 2$\sqrt{5}$ |
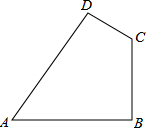 如图,已知在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系并加以证明.
如图,已知在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系并加以证明.
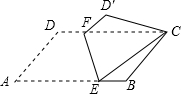 如图,将?ABCD折叠,使点A与C重合,折痕为EF.若∠A=60°,AD=4,AB=6,则AE的长为$\frac{19}{4}$.
如图,将?ABCD折叠,使点A与C重合,折痕为EF.若∠A=60°,AD=4,AB=6,则AE的长为$\frac{19}{4}$.