题目内容
12.如图,在平面直角坐标系中,点A、B的坐标分别为(-1,0),(3,0),现同时将点A、B分别向上平移2个单位,再向右平移1个单位,分别得到点A、B的对应点C、D,连接AC、BD、CD.(1)求点C、D的坐标及四边形ABDC的面积.
(2)在y轴上是否存在一点P,连接PA、PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.
(3)点P是线段CD上的一个动点,连接PA、PB,当点P在CD上移动时(不与C、D重合)给出下列结论:①$\frac{∠CAP+∠DBP}{∠APB}$的值不变;②$\frac{∠CAP+∠APB}{∠DBP}$的值不变;其中有且只有一个结论是正确的,请你找出这个结论并求其值.
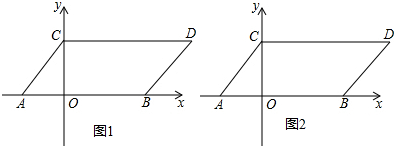
分析 (1)根据平移规律,直接得出点C,D的坐标,根据:四边形ABDC的面积=AB×OC求解;
(2)存在.设点P到AB的距离为h,则S△PAB=$\frac{1}{2}$×AB×h,根据S△PAB=S四边形ABDC,列方程求h的值,确定P点坐标.
(3)当点P在线段CD上,作PM∥AC交AB于点M,得到∠APM=∠CAP,因为AC∥BD,所以PM∥BD,得到∠BPM=∠DBP,所以∠APB=∠APM+∠BPM=∠CAP+∠DBP,即可解答.
解答 解:(1)依题意,得C(0,2),D(4,2),
∴S四边形ABDC=AB×OC=4×2=8;
(2)在y轴上是否存在一点P,使S△PAB=S四边形ABDC.理由如下:
设点P到AB的距离为h,
S△PAB=$\frac{1}{2}$×AB×h=2h,
由S△PAB=S四边形ABDC,得2h=8,
解得h=4,
∴P(0,4)或(0,-4).
(3)如图2,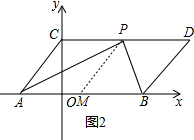
当点P在线段CD上,作PM∥AC交AB于点M,
∵PM∥AC,
∴∠APM=∠CAP,
∵AC∥BD,
∴PM∥BD,
∴∠BPM=∠DBP,
∴∠APB=∠APM+∠BPM=∠CAP+∠DBP,
∴$\frac{∠CAP+∠DBP}{∠APB}=1$,
故①正确.
点评 本题考查了坐标与图形平移的关系,坐标与平行四边形性质的关系及三角形、平行四边形的面积公式,解题的关键是理解平移的规律.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.有甲、乙、丙三种货物,若购甲3件,乙7件,丙1件,共需315元;若购甲4件,乙10件,丙1件,共需420元.现在购买甲、乙、丙各1件,共需( )
| A. | 105元 | B. | 210元 | C. | 170元 | D. | 不能确定 |
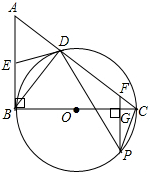 如图,已知,在△ABC中,∠ABC=90°,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
如图,已知,在△ABC中,∠ABC=90°,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.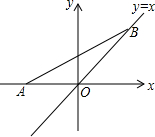 如图,点A的坐标为(-$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB最短时,求点B的坐标.
如图,点A的坐标为(-$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB最短时,求点B的坐标.
 如图,正六边形ABCDEF的边长为2,则对角线AC=2$\sqrt{3}$.
如图,正六边形ABCDEF的边长为2,则对角线AC=2$\sqrt{3}$.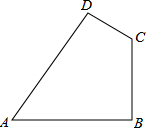 如图,已知在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系并加以证明.
如图,已知在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系并加以证明.