题目内容
19.计算:(1)$\frac{3a}{4b}$•$\frac{8b}{9{a}^{2}}$;
(2)$\frac{x{y}^{3}}{8{c}^{2}d}$÷$\frac{xy}{2c{d}^{2}}$;
(3)$\frac{a-b}{b}$•$\frac{ab}{2a-2b}$;
(4)$\frac{xy}{2x-3y}$•$\frac{6x-9y}{2{x}^{2}{y}^{2}}$.
分析 (1)根据分式的乘法,即可解答;
(2)根据分式的除法,即可解答;
(3)根据分式的乘法,即可解答;
(4)根据分式的乘法,即可解答.
解答 解:(1)原式=$\frac{2}{3a}$;
(2)原式=$\frac{x{y}^{3}}{8{c}^{2}d}•\frac{2c{d}^{2}}{xy}=\frac{{y}^{2}d}{4c}$;
(3)原式=$\frac{a-b}{b}•\frac{ab}{2(a-b)}=\frac{a}{2}$;
(4)原式=$\frac{xy}{2x-3y}•\frac{3(2x-3y)}{2{x}^{2}{y}^{2}}=\frac{3}{2xy}$.
点评 本题考查了分式的乘法和除法,解决本题的关键是进行约分.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
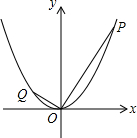 如图,已知点P是抛物线y=x2上的动点(点P在第一象限内),连结OP,过点O作OP的垂线交抛物线于另一点Q,当点P的横坐标是2时,点Q的坐标是(-$\frac{1}{2}$,$\frac{1}{4}$).
如图,已知点P是抛物线y=x2上的动点(点P在第一象限内),连结OP,过点O作OP的垂线交抛物线于另一点Q,当点P的横坐标是2时,点Q的坐标是(-$\frac{1}{2}$,$\frac{1}{4}$).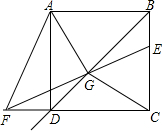 如图,正方形ABCD的边长为4,点E、F分别是射线BC和CD延长线上的动点,且BE=DF,连接EF与射线BD交于点G,连接AG、CG.
如图,正方形ABCD的边长为4,点E、F分别是射线BC和CD延长线上的动点,且BE=DF,连接EF与射线BD交于点G,连接AG、CG.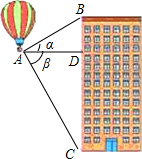 热气球的探测器显示,从热气球看一栋楼顶部的仰角α为27°,看这栋楼底部的俯角β为58°,热气球与这栋楼的水平距离为120米,这栋楼有多高(结果取整数)?
热气球的探测器显示,从热气球看一栋楼顶部的仰角α为27°,看这栋楼底部的俯角β为58°,热气球与这栋楼的水平距离为120米,这栋楼有多高(结果取整数)?