题目内容
10.在一个不透明的盒子里有3个小球,分别标有数字3,4,5,这些小球除所标数字不同外其余均相同,小英现从盒子里随机摸出1个小球,记下所标数字放回搅匀,再从盒子里随机摸出1个小球,用画树状图(或列表)的方法,求小英两次摸出的小球所标数字之积是奇数的概率.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与这两个球上的数字之和为奇数的情况,再利用概率公式求解即可求得答案.
解答 解:画树形图得:
由树形图可知:小英两次摸出的小球所标数字之积是奇数的概率=$\frac{4}{9}$.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
4.如果关于x,y的方程组$\left\{\begin{array}{l}{2x-y=10}\\{3x+y=5a}\end{array}\right.$的解满足x>0且y<0,请确定实数a的取值范围.
1.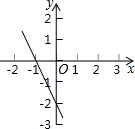 如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )
如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )
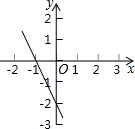 如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )
如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )| A. | x<-$\frac{1}{2}$ | B. | x>-$\frac{1}{2}$ | C. | x<-$\frac{1}{4}$ | D. | x>-$\frac{1}{4}$ |
20.在平面直角坐标系中,已知点A(2,3),则点A关于x轴的对称点坐标为( )
| A. | (2,-3) | B. | (3,2) | C. | (-2,3) | D. | (-2,-3) |
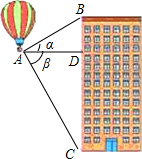 热气球的探测器显示,从热气球看一栋楼顶部的仰角α为27°,看这栋楼底部的俯角β为58°,热气球与这栋楼的水平距离为120米,这栋楼有多高(结果取整数)?
热气球的探测器显示,从热气球看一栋楼顶部的仰角α为27°,看这栋楼底部的俯角β为58°,热气球与这栋楼的水平距离为120米,这栋楼有多高(结果取整数)?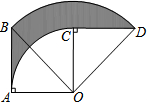 如图,在Rt△OAB中,∠AOB=45°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为π.
如图,在Rt△OAB中,∠AOB=45°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为π. 如图,反比例函数y=$\frac{6}{x}$在一象限的图象上有两点A,B,它们的横坐标分别为1,3,则△OAB的面积为8.
如图,反比例函数y=$\frac{6}{x}$在一象限的图象上有两点A,B,它们的横坐标分别为1,3,则△OAB的面积为8.