题目内容
已知两列数:2,5,8,11,14,17,…,2+(200-1)×3 和 5,9,13,17,21,25,…,5+(200-1)×4 都有200项,这两列数中相同的项数有 .
考点:规律型:数字的变化类
专题:
分析:第一个数列公差为3,第二个数列公差为4,第一个相同的项数是5,下面的相同的数就是以5为首项,以12为公差的数列,进一步分析探讨得出答案即可.
解答:解:第一个相同的项数是5,第一个数列的公差为3,第二个数列中公差为4,也就是说,第二个相同的数减去5即是3的倍数,又是4的倍数,
下面的相同的数就是以5为首项,以12为公差的数列:5、17、29…
第一个数列最大为2+(200-1)×3=599;
第二个数列最大为5+(200-1)×4=801;
新数列最大不能超过599,
因为5+12×49=593,5+12×50=605,
所以共有50个相同的项数.
故答案为:50个.
下面的相同的数就是以5为首项,以12为公差的数列:5、17、29…
第一个数列最大为2+(200-1)×3=599;
第二个数列最大为5+(200-1)×4=801;
新数列最大不能超过599,
因为5+12×49=593,5+12×50=605,
所以共有50个相同的项数.
故答案为:50个.
点评:此题考查数字的变化规律,找出数字之间的联系,得出规律,解决问题.

练习册系列答案
相关题目
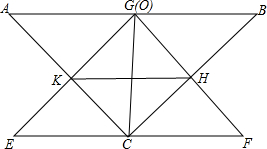 如图所示,在△ABC中,AC=BC,∠ACB=90°,O为AB的中点,现将一个三角板EGF的直角顶点G放在点O处,把△EFG绕点O旋转,EG交直线AC于点K,FG交直线BC于点H.
如图所示,在△ABC中,AC=BC,∠ACB=90°,O为AB的中点,现将一个三角板EGF的直角顶点G放在点O处,把△EFG绕点O旋转,EG交直线AC于点K,FG交直线BC于点H.