题目内容
某商场服装部为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售目标,根据目标完成的情况对营业员进行适当的奖惩.为了确定一个适当的目标,商场统计了每个营业员在某月的销售额(单位:万元),列统计表如下;
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均的月销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
(3)如果想让一半左右的营业员都能达到目标,你认为月销售额定为多少合适?说明理由.
| 销售额(万元) | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 频数(人数) | 1 | 1 | 5 | 4 | 3 | 2 | 3 |
| 销售额(万元) | 22 | 23 | 24 | 26 | 28 | 30 | 32 |
| 频数(人数) | 1 | 1 | 1 | 2 | 3 | 1 | 2 |
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
(3)如果想让一半左右的营业员都能达到目标,你认为月销售额定为多少合适?说明理由.
考点:频数(率)分布表
专题:
分析:(1)根据题意分别求出众数、中位数和平均数;
(2)从平均数、中位数、众数中,选择较大的;
(3)根据众数、中位数和平均数的意义回答.
(2)从平均数、中位数、众数中,选择较大的;
(3)根据众数、中位数和平均数的意义回答.
解答:解:(1)分析数据:样本中,15出现的次数最多;故样本众数为15,所以月销售额在15万元人数最多;
将数据从小到大排列,找最中间的两个数都为18,故中位数是18,所以中间的月销售额是18万元;
根据平均数的求法:平均数为
(13+14+15×5+16×4+17×3+18×2+19×3+22+23+24+26×2+28×3+30+32×2)=
×609=20.3(万元);
故这组数据的平均数是20.3,所以平均的月销售额是20.3万元;
(2)如果想确定一个较高的目标,这个目标可以定为20.3万元(平均数),
因为从平均数、中位数、众数中,平均数最大.
故月销售额定为每月20.3万元是一个较高的目标,大约会有
的营业员获得奖励;
(3)如果想让一半左右的营业员都能达到目标,月销售额可以定为18万元(中位数),
因为从样本情况看,月销售额在18万元以上(含18万元)的有16人,占总人数的一半左右,
故每月销售额定为18万元,可以估计有一半左右的营业员获得奖励.
将数据从小到大排列,找最中间的两个数都为18,故中位数是18,所以中间的月销售额是18万元;
根据平均数的求法:平均数为
| 1 |
| 30 |
| 1 |
| 30 |
故这组数据的平均数是20.3,所以平均的月销售额是20.3万元;
(2)如果想确定一个较高的目标,这个目标可以定为20.3万元(平均数),
因为从平均数、中位数、众数中,平均数最大.
故月销售额定为每月20.3万元是一个较高的目标,大约会有
| 1 |
| 3 |
(3)如果想让一半左右的营业员都能达到目标,月销售额可以定为18万元(中位数),
因为从样本情况看,月销售额在18万元以上(含18万元)的有16人,占总人数的一半左右,
故每月销售额定为18万元,可以估计有一半左右的营业员获得奖励.
点评:本题考查的是平均数、众数和中位数的定义及运用.要学会根据统计量的意义分析解决问题.

练习册系列答案
相关题目
 如图,已知等腰△ABC中,AB=AC,CD、BE分别是AB、AC边上的高,则图中的全等的三角形共有( )
如图,已知等腰△ABC中,AB=AC,CD、BE分别是AB、AC边上的高,则图中的全等的三角形共有( )| A、1对 | B、2对 | C、3 | D、4对 |
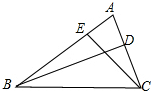 如图,在△ABC中,已知BD、CE是△ABC的高,试说明B、C、D、E四点在同一圆上.
如图,在△ABC中,已知BD、CE是△ABC的高,试说明B、C、D、E四点在同一圆上.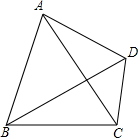 如图所示,四边形ABCD中,∠BAD+∠BCD=180°,求证:∠BAC=∠BDC.
如图所示,四边形ABCD中,∠BAD+∠BCD=180°,求证:∠BAC=∠BDC. 如图,△ABC中,BE平分∠ABC,DE∥BC交AB于D,AC=12,AB=9,AE=4,求DE的值.
如图,△ABC中,BE平分∠ABC,DE∥BC交AB于D,AC=12,AB=9,AE=4,求DE的值.