题目内容
在△ABC中,已知A(4,1),B(7,5),C(-4,7),试判断△ABC的形状.
考点:勾股定理的逆定理,坐标与图形性质,两点间的距离公式
专题:
分析:先利用两点间的距离公式求出AB2、BC2、AC2,再根据勾股定理的逆定理即可判断△ABC的形状.
解答:解:∵A(4,1),B(7,5),C(-4,7),
∴AB2=(7-4)2+(5-1)2=25,
BC2=(-4-7)2+(7-5)2=125,
AC2=(-4-4)2+(7-1)2=100,
∴AB2+AC2=BC2,
∴△ABC是直角三角形.
∴AB2=(7-4)2+(5-1)2=25,
BC2=(-4-7)2+(7-5)2=125,
AC2=(-4-4)2+(7-1)2=100,
∴AB2+AC2=BC2,
∴△ABC是直角三角形.
点评:本题考查了两点间的距离公式,坐标与图形性质,勾股定理的逆定理,正确求出AB2、BC2、AC2是解题的关键.

练习册系列答案
相关题目
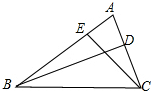 如图,在△ABC中,已知BD、CE是△ABC的高,试说明B、C、D、E四点在同一圆上.
如图,在△ABC中,已知BD、CE是△ABC的高,试说明B、C、D、E四点在同一圆上. 如图,△ABC中,BE平分∠ABC,DE∥BC交AB于D,AC=12,AB=9,AE=4,求DE的值.
如图,△ABC中,BE平分∠ABC,DE∥BC交AB于D,AC=12,AB=9,AE=4,求DE的值.