Question

19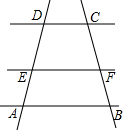．如图，AB∥CD，AB=a，CD=b，点E、F分别在AD、BC上，且EF∥AB，设EF到CD、AB的距离为d₁、d₂，则有：
当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{1}{1}$时，有EF=$\frac{a+b}{2}$；
当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{1}{2}$时，有EF=$\frac{a+2b}{3}$；
当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{2}{1}$时，有EF=$\frac{2a+b}{3}$；
当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{3}{1}$时，有EF=$\frac{3a+b}{4}$；
当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{4}{1}$时，有EF=$\frac{4a+b}{5}$；当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{5}{1}$时，有EF=$\frac{5a+b}{6}$；
（1）当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{1}{n}$时，有EF=$\frac{a+nb}{n+1}$；当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{m}{1}$时，有EF=$\frac{ma+b}{m+1}$；（m，n均为正整数）
（2）猜想当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{m}{n}$时，有EF=$\frac{ma+nb}{m+n}$，并证明你的猜想．

Answer 1

分析 作DN⊥AB于N，交EF于M作DH∥BC，分别交EF、AB于G、H点，如图，利用平行线的性质得到DM⊥EF，则DM=d₁，MN=d₂，CD=GF=BH，所以AH=AB-CD=a-b，EF=EG+CD=EG+b，
（1）当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{1}{n}$时，根据平行线分线段成比例定理，由EG∥AH得到$\frac{EG}{AH}$=$\frac{DM}{DN}$=$\frac{{d}_{1}}{{d}_{1}+{d}_{2}}$=$\frac{1}{n+1}$，则EG=$\frac{1}{n+1}$（a-b），所以EF=$\frac{a+nb}{n+1}$；当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{m}{1}$时，$\frac{EG}{AH}$=$\frac{DM}{DN}$=$\frac{{d}_{1}}{{d}_{1}+{d}_{2}}$=$\frac{m}{m+1}$，则有EF=$\frac{ma+b}{m+1}$；
（2）当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{m}{n}$时，$\frac{EG}{AH}$=$\frac{DM}{DN}$=$\frac{{d}_{1}}{{d}_{1}+{d}_{2}}$=$\frac{m}{m+n}$，则EG=$\frac{m}{m+n}$（a-b），所以EF=$\frac{m}{m+n}$（a-b）+b=$\frac{ma+nb}{m+n}$．

解答 解：作DN⊥AB于N，交EF于M，作DH∥BC，分别交EF、AB于G、H点，如图，
∵EF∥CD，
∴DM⊥EF，
∴DM=d₁，MN=d₂，
∵DC∥GF∥BH，
∵CD=GF=BH，
∴AH=AB-CD=a-b，EF=EG+CD=EG+b，
（1）当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{1}{n}$时，
∵EG∥AH，
∴$\frac{EG}{AH}$=$\frac{DM}{DN}$=$\frac{{d}_{1}}{{d}_{1}+{d}_{2}}$=$\frac{1}{n+1}$，
∴EG=$\frac{1}{n}$（a-b），
∴EF=$\frac{1}{n+1}$（a-b）+b=$\frac{a+nb}{n+1}$；
当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{m}{1}$时，
∵EG∥AH，
∴$\frac{EG}{AH}$=$\frac{DM}{DN}$=$\frac{{d}_{1}}{{d}_{1}+{d}_{2}}$=$\frac{m}{m+1}$，
∴EG=$\frac{m}{m+1}$（a-b），
∴EF=$\frac{m}{m+1}$（a-b）+b=$\frac{ma+b}{m+1}$；
（2）当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{m}{n}$时，有EF=，理由如下：
∵EG∥AH，
∴$\frac{EG}{AH}$=$\frac{DM}{DN}$=$\frac{{d}_{1}}{{d}_{1}+{d}_{2}}$=$\frac{m}{m+n}$，
∴EG=$\frac{m}{m+n}$（a-b），
∴EF=$\frac{m}{m+n}$（a-b）+b=$\frac{ma+nb}{m+n}$．
故答案为：$\frac{a+nb}{n+1}$；$\frac{ma+b}{m+1}$；$\frac{ma+nb}{m+n}$．

点评 本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边．也考查了比例的性质．