题目内容
13. 已知:如图,D、E、F是△ABC各边的中点,FG∥CD交ED的延长线于点G,AC=6.求GD的长度.
已知:如图,D、E、F是△ABC各边的中点,FG∥CD交ED的延长线于点G,AC=6.求GD的长度.
分析 根据中位线定理得:DE∥AC,则四边形GDCF是平行四边形,所以GD=CF=$\frac{1}{2}$AC.
解答 证明:∵D、E、F是△ABC各边的中点,
∴DE是△ABC的中位线,$CF=\frac{1}{2}AC=3$,
∴DE∥AC,
即GD∥FC,
∵FG∥CD,
∴四边形GDCF为平行四边形,
∴CF=GD=3.
点评 本题考查了三角形的中位线定理、平行四边形的性质和判定,根据平行四边形的对边相等,将DG转化为CF的长,而CF是已知线段的一半,从而求出结论.

练习册系列答案
相关题目
3.若△ABC∽△A′B′C′,∠A=20°,∠C=120°,则∠B′的度数为( )
| A. | 20° | B. | 30° | C. | 40° | D. | 120° |
 如图,在△ABC中,AD⊥BC,垂足为D,E为AC上一点,BE交AD于F,且BF=AC,FD=CD,AD=3,求AB的长.
如图,在△ABC中,AD⊥BC,垂足为D,E为AC上一点,BE交AD于F,且BF=AC,FD=CD,AD=3,求AB的长.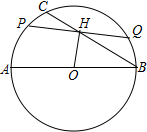 在⊙O中,直径AB=8,∠ABC=30°,点H在弦BC上,弦PQ⊥OH于点H.当点P在$\widehat{AC}$上移动时,PQ长的最大值为4$\sqrt{3}$.
在⊙O中,直径AB=8,∠ABC=30°,点H在弦BC上,弦PQ⊥OH于点H.当点P在$\widehat{AC}$上移动时,PQ长的最大值为4$\sqrt{3}$. 如图,已知∠AOB=30°,点P在边OA上,点M、N在边OB上,且PM=PN=10,MN=12,则OP=16.
如图,已知∠AOB=30°,点P在边OA上,点M、N在边OB上,且PM=PN=10,MN=12,则OP=16. 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=25°,那么∠2的度数是20°.
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=25°,那么∠2的度数是20°.