题目内容
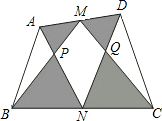 如图,M、N为四边形ABCD的边AD、BC的中点,AN、BM交于P点,CM、DN交于Q点.若四边形ABCD的面积为150,四边形MPNQ的面积为50,求阴影部分的面积之和.
如图,M、N为四边形ABCD的边AD、BC的中点,AN、BM交于P点,CM、DN交于Q点.若四边形ABCD的面积为150,四边形MPNQ的面积为50,求阴影部分的面积之和.考点:面积及等积变换
专题:
分析:首先连接BD,利用S△ABM=S△BDM,S△BDN=S△CDN,得出S四边形BMDN=
S四边形ABCD,进而得出S四边形ANCM=
S四边形ABCD,再利用S四边形ANCM+S四边形BMDN=S四边形ABCD,即可得出S四边形MPNQ=S△ABP+S△CDQ,即可得出阴影部分的面积之和.
| 1 |
| 2 |
| 1 |
| 2 |
解答: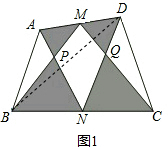 解:连接BD.
解:连接BD.
∵M、N是AD、BC中点,
∴S△ABM=S△BDM,S△BDN=S△CDN,(等底同高的两个三角形面积相等)
∴S四边形BMDN=
S四边形ABCD.
同理,S四边形ANCM=
S四边形ABCD.
∴S四边形ANCM+S四边形BMDN=S四边形ABCD,
∴S四边形MPNQ=S△ABP+S△CDQ,
∴阴影部分的面积为:S阴影=S四边形ABCD-S四边形MPNQ-(S△ABP+S△CDQ)=150-50×2=50.
 解:连接BD.
解:连接BD.∵M、N是AD、BC中点,
∴S△ABM=S△BDM,S△BDN=S△CDN,(等底同高的两个三角形面积相等)
∴S四边形BMDN=
| 1 |
| 2 |
同理,S四边形ANCM=
| 1 |
| 2 |
∴S四边形ANCM+S四边形BMDN=S四边形ABCD,
∴S四边形MPNQ=S△ABP+S△CDQ,
∴阴影部分的面积为:S阴影=S四边形ABCD-S四边形MPNQ-(S△ABP+S△CDQ)=150-50×2=50.
点评:此题主要考查了面积及等积变换,利用已知得出S四边形BMDN=
S四边形ABCD与S四边形ANCM=
S四边形ABCD是解题关键.
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目
 如图,已知△ABC中,AD平分∠BAC.∠C=20°,AB+BD=AC,则∠B的度数是
如图,已知△ABC中,AD平分∠BAC.∠C=20°,AB+BD=AC,则∠B的度数是 如图,在△ABC中,∠B=60°,AB=10,BC=12,则边AC=
如图,在△ABC中,∠B=60°,AB=10,BC=12,则边AC=