题目内容
解方程:
+
+
=0.
| x-2011 |
| 1999 |
| 1-x |
| 2010 |
| x-2 |
| 2009 |
考点:解一元一次方程
专题:计算题
分析:将含x的项放在左边,常数项移到右边,然后通分化简即可得出答案.
解答:解:原方程可化为:
=
,
整理得:(2010×2009+1999)x=2011×2010×2009+1999(4020-2009),
即(2010×2009+1999)x=2011×(2010×2009+1999),
解得:x=2011.
| 2010(1999+2009)x |
| 1999×2010×2009 |
| 2011×2010×2009+2×1999×2010-1999×2009 |
| 1999×2010×2009 |
整理得:(2010×2009+1999)x=2011×2010×2009+1999(4020-2009),
即(2010×2009+1999)x=2011×(2010×2009+1999),
解得:x=2011.
点评:此题考查了解一元一次方程的知识,本题分母较大,不要按照常规方法进行求解,要注意仔细观察寻找解题技巧,有一定难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
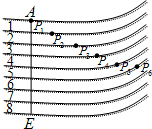
 跳格游戏如图:人从格外进入格中,每次可向前跳1格或2格,那么人从格外跳到第6格可以有( )种方法.
跳格游戏如图:人从格外进入格中,每次可向前跳1格或2格,那么人从格外跳到第6格可以有( )种方法.| A、6 | B、8 | C、13 | D、15 |
小明掷一个质地均匀的正方体的骰子,骰子的六个面分别刻有1到6的点数,下列说法错误的是( )
| A、“正面出现点数大于6”是不可能事件 | ||
| B、“正面出现点数大于0”是必然事件 | ||
C、“正面出现点数是1”的概率是
| ||
D、“正面出现点数是偶数”的概率是
|
 在田径比赛中的标准跑道一般是由长为85.96米的两条直道和半径为36米的两条半圆弧跑道组成.标准跑道分为8道,每条跑道宽1.25米.国际田联规定:
在田径比赛中的标准跑道一般是由长为85.96米的两条直道和半径为36米的两条半圆弧跑道组成.标准跑道分为8道,每条跑道宽1.25米.国际田联规定: 如图,四边形ABCD的对角线AC、BD相交于点O,
如图,四边形ABCD的对角线AC、BD相交于点O, 如图,A、B、E、C四点都在⊙O上,AD是△ABC的高,∠CAD=∠EAB,AE是⊙O的直径吗?为什么?
如图,A、B、E、C四点都在⊙O上,AD是△ABC的高,∠CAD=∠EAB,AE是⊙O的直径吗?为什么?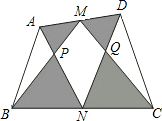 如图,M、N为四边形ABCD的边AD、BC的中点,AN、BM交于P点,CM、DN交于Q点.若四边形ABCD的面积为150,四边形MPNQ的面积为50,求阴影部分的面积之和.
如图,M、N为四边形ABCD的边AD、BC的中点,AN、BM交于P点,CM、DN交于Q点.若四边形ABCD的面积为150,四边形MPNQ的面积为50,求阴影部分的面积之和.