题目内容
 如图,已知△ABC中,AD平分∠BAC.∠C=20°,AB+BD=AC,则∠B的度数是
如图,已知△ABC中,AD平分∠BAC.∠C=20°,AB+BD=AC,则∠B的度数是考点:全等三角形的判定与性质
专题:
分析:在AC上取一点E,使AE=AB,连接DE,则有EC=BD,证△ABD≌△AED,可以得出∠B=∠AED,BD=DE,则有DE=EC,∠EDC=∠C=20°,∠AED=40°,得出结论.
解答:解:在AC上取一点E,使AE=AB,连接DE.
∵AB+BD=AC,
∴BD=AC-AB,
即BD=CE.
∵AD平分∠BAC,
∴∠BAD=∠EAD,
在△ABD和△AED中,
∴△ABD≌△AED,
∴BD=DE,∠B=∠AED,
∴DE=EC,
∴∠C=∠EDC,
∵∠C=20°,
∴∠EDC=20°,
∵∠AED=∠C+∠EDC,
∴∠AED=20°+20°=40°
∴∠B=40°.
故答案为:40°

∵AB+BD=AC,
∴BD=AC-AB,
即BD=CE.
∵AD平分∠BAC,
∴∠BAD=∠EAD,
在△ABD和△AED中,
|
∴△ABD≌△AED,
∴BD=DE,∠B=∠AED,
∴DE=EC,
∴∠C=∠EDC,
∵∠C=20°,
∴∠EDC=20°,
∵∠AED=∠C+∠EDC,
∴∠AED=20°+20°=40°
∴∠B=40°.
故答案为:40°

点评:本题考查了截取法作辅助线的方法的运用,等腰三角形的性质,全等三角形的判定及性质,三角形的外角与内角的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

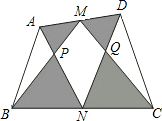 如图,M、N为四边形ABCD的边AD、BC的中点,AN、BM交于P点,CM、DN交于Q点.若四边形ABCD的面积为150,四边形MPNQ的面积为50,求阴影部分的面积之和.
如图,M、N为四边形ABCD的边AD、BC的中点,AN、BM交于P点,CM、DN交于Q点.若四边形ABCD的面积为150,四边形MPNQ的面积为50,求阴影部分的面积之和.