题目内容
15．方程组$\left\{\begin{array}{l}{\frac{x+y}{2}=\frac{y+z}{4}=\frac{x+z}{3}}\\{x+y+z=27}\end{array}\right.$中，x=3，y=8，z=15．分析 设$\frac{x+y}{2}$=$\frac{y+z}{4}$=$\frac{x+z}{3}$=k，则x+y=2k，y+z=4k，x+z=3k，求出2x+2y+2z=9k，即可求出k，得出方程组，求出方程组的解即可．
解答 解：设$\frac{x+y}{2}$=$\frac{y+z}{4}$=$\frac{x+z}{3}$=k，
则x+y=2k，y+z=4k，x+z=3k，
2x+2y+2z=9k，
∵x+y+z=27，
∴9k=54，
k=6，
即$\left\{\begin{array}{l}{x+y=12}\\{y+z=24}\\{x+z=18}\end{array}\right.$，
解得：x=3，y=8，z=15，
故答案为：3，8，15．
点评 本题考查了解三元一次方程组，能求出k的值是解此题的关键．
练习册系列答案
相关题目
10．
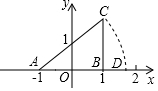如图，Rt△ABC的边AB在x轴上，且A（-1，0），B（1，0），∠A=45°，斜边AC以点A为旋转中心，顺时针旋转45°，恰好与x轴相交于D，则点D的坐标是（ ）
如图，Rt△ABC的边AB在x轴上，且A（-1，0），B（1，0），∠A=45°，斜边AC以点A为旋转中心，顺时针旋转45°，恰好与x轴相交于D，则点D的坐标是（ ）| A． | （$\sqrt{2}$，0） | B． | （2$\sqrt{2}$，0） | C． | （2$\sqrt{2}$-1，0） | D． | （2$\sqrt{2}$-2，0） |
如图，抛物线y=-$\frac{1}{4}$x2-$\frac{1}{2}$x+$\frac{3}{4}$与x轴交于A，C两点（点A在点C的左边）．直线y=kx+b（k≠0）分别交x轴，y轴于A，B两点，且除了点A之外，该直线与抛物线没有其它任何交点．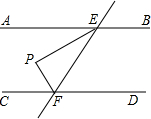
如图，AB∥CD，直线EF与AB，CD分别相交于点E、F，EP平分∠AEF，FP平分∠EFC．