题目内容
材料:一般地,n个相同的因数a相乘:
记为an.
如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).
一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
问题:(1)log24、log216、log264之间满足的等量关系是 ;
(2)猜测结论:logaM+logaN= (a>0且a≠1,M>0,N>0)
(3)根据幂的运算法则:an•am=an+m以及对数的含义说明(2)中你得出的结论.
| ||
| n个 |
如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).
一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
问题:(1)log24、log216、log264之间满足的等量关系是
(2)猜测结论:logaM+logaN=
(3)根据幂的运算法则:an•am=an+m以及对数的含义说明(2)中你得出的结论.
考点:同底数幂的乘法,幂的乘方与积的乘方
专题:阅读型,新定义
分析:(1)根据同底数幂乘法,可得答案;
(2)根据规律,可得答案;
(3)根据同底数幂的乘法,可得证明结论.
(2)根据规律,可得答案;
(3)根据同底数幂的乘法,可得证明结论.
解答:解:(1)log24、log216、log264之间满足的等量关系是 log24+log216=log264;
(2)猜测结论:logaM+logaN=logaMN(a>0且a≠1,M>0,N>0)
(3)设X=logaM,Y=logaN,
根据对数的含义:aX=M,aY=N,
根据幂的运算法则:M•N=aX•aY=aX+Y,
根据对数的含义:X+Y=logaM•N,
logaM+logaN=X+Y=logaax+y=log aax•ay=logaMN.
(2)猜测结论:logaM+logaN=logaMN(a>0且a≠1,M>0,N>0)
(3)设X=logaM,Y=logaN,
根据对数的含义:aX=M,aY=N,
根据幂的运算法则:M•N=aX•aY=aX+Y,
根据对数的含义:X+Y=logaM•N,
logaM+logaN=X+Y=logaax+y=log aax•ay=logaMN.
点评:本题考查了同底数幂的乘法,利用同底数幂的乘法,乘方与对数的关系.

练习册系列答案
相关题目

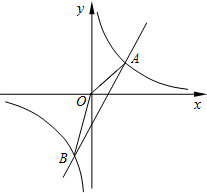 如图,已知反比例函数y1=
如图,已知反比例函数y1= 如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(1,1),
如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(1,1),