题目内容
14. 如图.△ABC中,∠B=∠C,点P、Q、R分别在AB、BC、AC上,且PB=QC,QB=RC.
如图.△ABC中,∠B=∠C,点P、Q、R分别在AB、BC、AC上,且PB=QC,QB=RC.求证:点Q在PR的垂直平分线上.
分析 根据全等三角形的判定定理证明△BQP≌△CRQ,得到QP=QR,根据线段的垂直平分线的判定证明结论.
解答  证明:连接PQ,
证明:连接PQ,
在△BQP和△CRQ中,
$\left\{\begin{array}{l}{PB=QC}\\{∠B=∠C}\\{QB=RC}\end{array}\right.$,
∴△BQP≌△CRQ,
∴QP=QR,
∴点Q在PR的垂直平分线上.
点评 本题考查的是三角形全等的判定和性质以及线段的垂直平分线的判定,掌握到线段的两个端点的距离相等的点在线段的垂直平分线上是解题的关键.

练习册系列答案
相关题目
19.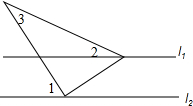 如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )
如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )
 如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )
如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )| A. | 26°40′ | B. | 27°20′ | C. | 27°40′ | D. | 73°20′ |
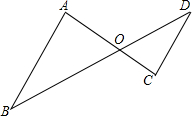 如图,若∠A=∠C,那么△OAB与△OCD相似吗?有OA•OD=OB•OC吗?为什么?
如图,若∠A=∠C,那么△OAB与△OCD相似吗?有OA•OD=OB•OC吗?为什么?
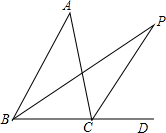 如图,BP,CP分别平分∠ABD,∠ACD,若∠A=40°,求∠P.
如图,BP,CP分别平分∠ABD,∠ACD,若∠A=40°,求∠P. 如图,在△ABC中,分别画出线段AB、BC的垂直平分线上l1、l2相交于点O,求证:点O在AC的垂直平分线上.
如图,在△ABC中,分别画出线段AB、BC的垂直平分线上l1、l2相交于点O,求证:点O在AC的垂直平分线上. 如图,在△ABC中,DE垂直平分BC,F为CD中点,求证:EF∥AB.
如图,在△ABC中,DE垂直平分BC,F为CD中点,求证:EF∥AB.