题目内容
19.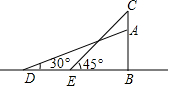 如图,小山AB的顶上有一高20m的铁塔(CA),在山脚平地上的D点,测得山顶A的仰角为30°,在E点测得塔尖C的仰角为45°(点D、E、B在一条直线上),已知DE=60m.求山高AB.(结果保留根号)
如图,小山AB的顶上有一高20m的铁塔(CA),在山脚平地上的D点,测得山顶A的仰角为30°,在E点测得塔尖C的仰角为45°(点D、E、B在一条直线上),已知DE=60m.求山高AB.(结果保留根号)
分析 设AB=xm,根据直角三角形的性质得到EB=CB,根据正切的定义列出算式,计算即可.
解答 解:设AB=xm,则BC=(x+20)m,
∵∠CEB=45°,
∴EB=CB=x+20,
则DE=x+20+60,
tan∠ADB=$\frac{AB}{DB}$,即$\frac{\sqrt{3}}{3}$=$\frac{x}{x+80}$,
解得,x=40$\sqrt{3}$+40,
答:山高AB为(40$\sqrt{3}$+40)m.
点评 此题考查了解直角三角形的应用仰角俯角的问题,掌握仰角俯角的定义、特殊角的三角函数值是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
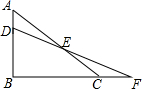 已知:如图,在△ABC中,点D在边AB上,且AD=$\frac{1}{3}$AB.点F在边BC的延长线上,连结DF,交AC于点E,设$\frac{CF}{BF}$=k.求:$\frac{CE}{AE}$的值.
已知:如图,在△ABC中,点D在边AB上,且AD=$\frac{1}{3}$AB.点F在边BC的延长线上,连结DF,交AC于点E,设$\frac{CF}{BF}$=k.求:$\frac{CE}{AE}$的值.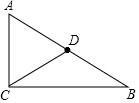 如图,在Rt△ABC中,∠C=90°,AC=9cm,BC=12cm,点D是AB的中点,现在以C点为圆心画圆,使A,B,D三点满足一点在⊙C外,一点在⊙C上,一点在⊙C内,求⊙C的半径.
如图,在Rt△ABC中,∠C=90°,AC=9cm,BC=12cm,点D是AB的中点,现在以C点为圆心画圆,使A,B,D三点满足一点在⊙C外,一点在⊙C上,一点在⊙C内,求⊙C的半径.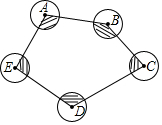 如图,⊙A、⊙B、⊙C、⊙D、⊙E的半径都是4cm,顺次连接五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)面积的和为24πcm2.
如图,⊙A、⊙B、⊙C、⊙D、⊙E的半径都是4cm,顺次连接五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)面积的和为24πcm2. 如图,若圆心角为108°的弧度的长度为18πcm,则它的半径为30cm.
如图,若圆心角为108°的弧度的长度为18πcm,则它的半径为30cm.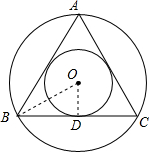 已知,正三角形ABC的边长为1,正三角形ABC的外接圆和它的内切圆是同心圆,求这两个圆所形成的圆环的面积.
已知,正三角形ABC的边长为1,正三角形ABC的外接圆和它的内切圆是同心圆,求这两个圆所形成的圆环的面积.